Imputing Missing Data in Clinical Trials

Missing data is inevitable for several reasons during the clinical trials. As we know, missing data can be classified into one of three categories, like MCAR(Missing Completely At Random), MAR(Missing At Random) and MNAR(Missing Not At Random).

Here we don't talk about how to determine which type of missingness your data have, you can refer to the articles Multiple Imputation.

Or a summary (Missing data assumptions and corresponding imputation methods) in Multiple imputation as a valid way of dealing with missing data

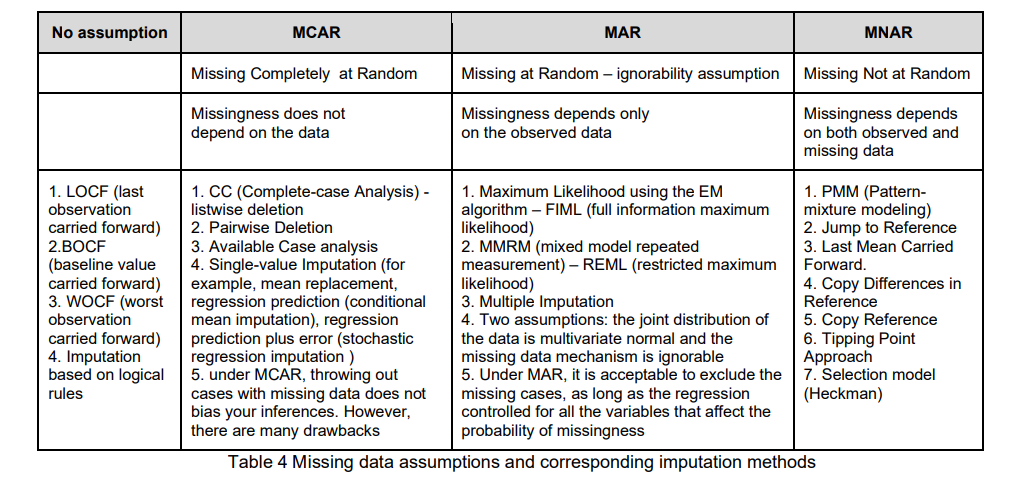
Let's keep it more practical and focus on how to impute missing data. For example, LOCF (Last Observation Carry Forward) is the standard method for imputing missing data in clinical trial studies. It is used to fill in missing values at a later point in the study, but that can lead to biased results. Other methods such as BOCF(Baseline Observation Carry Forward), WOCF(Worsts Observation Carry forward), and Multiple Imputation are also used, but rarely seen in oncology studies. The last common method like MMRM(Mixed-Effect Model Repeated Measure) is used for continuous missing data.

Given SAS is still the dominant delivery program, here I will record how to use SAS to handle this missing data. However I also perfectly suggest using R as the alternative program or QC program, as I believe R will be accepted by regulatory authorities, at least as an optional delivery program. Therefore I'm gonna record how to use the rbmi package to deal with missing data like LOCF and multiple imputation, and compute the LS means with ANCOVA model in another article.

LOCF

Here we create a dummy dataset with 3 columns: usubjid, avisitn and aval.

data data;
    input usubjid $8. avisitn aval;
    datalines;
1001-101 0 85
1001-101 1 84
1001-101 2 86
1001-101 3 .
1001-101 4 .
1001-101 5 85
1002-101 0 90
1002-101 1 .
1002-101 2 91
1002-101 3 92
1002-101 4 .
1002-101 5 .
;
run;
proc sort; by usubjid avisitn; run;

Actually there are several methods to implement the LOCF, referring to LOCF-Different Approaches, Same Results Using LAG Function, RETAIN Statement, and ARRAY Facility. I usually use the RETAIN statement as it's easy to understand and also very elegant. So this brings us to the final code, once the usubjid changes, the rn variable will be initialized to null(.) or first aval grouped by usubjid. And then through the if statement to check if the next aval is not missing, and carry the rn forward to the next aval.

data locf;
    length dtype $10.;
    retain rn;
    set data;
    by usubjid avisitn;
    
    if first.usubjid then rn=.;
    if aval ne . then do;
        rn=aval;
        aval_locf=aval;
    end;
    else do;
        aval_locf=rn;
        dtype="LOCF";
    end;
run;

We can see the final dataset below with LOCF'ed variable, aval_LOCF.

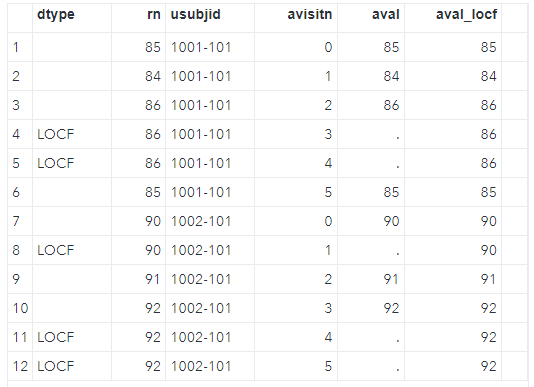
And the BOCF and WOCF methods are also conservative like LOCF, and their programming logic is roughly the same. The former one can be used when subjects drop out due to Adverse Event, while the latter one can be used for lack of efficacy(LOE) indeed.

Multiple Imputation

For Multiple Imputation(MI), it's more robust than LOCF, as it has multiple imputations.

The procedures for Multiple Imputation are generally the same in both SAS and R, such as:

Impution, the missing data is imputed m times and generates m complete datasets with a specified model or distribution.
Analysis, each of these datasets is analyzed using a certain statistical model or function, and generating m sets of estimates.
Pooling, the m sets of estimates are combined to one MI result with an appropriate method, like Rubin´s Rules (RR) that is specifically designed to pool parameter estimates and is also wrapped into SAS and R packages.

These procedures are easy to understand, so how to implement them?

In SAS, you can use proc mi procedure for imputation, select one statistical model, such as proc mixed for analysis, and lastly use proc mianalyze procedure for pooling.
In R, although there are several R packages available for use, I personally prefer using mice and rmbi packages, which will be introduced in other articles.

MMRM

Compared to the above two methods, the MMRM (Mixed-effect Model for Repeated Measures) method does not do the imputation for individual missing data, while treating each individual as a random effect, as it has already considered the missing data in the model(that the missing data is implicitly imputed).

So it can be seen that MMRM does well in controlling type I error but LOCF may lead to the inflation of type I error. Although the MI method can also control Type I error, it is more conservative than MMRM because it will underestimate the treatment effect.

Actually there is really impressive article that talks about the comparison of MMRM versus MI, as well as the regulatory authorities' considerations on this topic. Referring to it would be quite helpful. Handling of Missing Data: Comparison of MMRM (mixed model repeated measures) versus MI (multiple imputation).

In SAS, you can simply use proc mixed procedure using mixed model with maximum likelihood-based method.
In R, the nlme package is commonly used, but the new mmrm package offers advanced functionality (just heard before...).

Reference

Multiple Imputation
SAS LOCF For Multiple Variables
SAS LOCF
LOCF-Different Approaches, Same Results Using LAG Function, RETAIN Statement, and ARRAY Facility
LOCF Method and Application in Clinical Data Analysis
临床试验中缺失数据的预防与处理
 Handling of Missing Data: Comparison of MMRM (mixed model repeated measures) versus MI (multiple imputation)