一般我们是将检测结果跟临床金标准进行比较,常见的诊断指标如灵敏度、特异度、阳性预测值和阴性预测值等。但是当在方法学比较没有临床金标准(即对照方法不是临床金标准)时,那么我们就无法估计其实际的灵敏度和特异度,此时可以考虑用阳性一致性(positive percent agreement, PPA)和阴性一致性(negative percent agreement, NPA),这种情况还是比较常见的(比如在组织诊断中)
有时还会使用总体一致性(overall percent agreement, OPA),但是这个有时会有误导,所以主要还是看PPA和NPA;列联表如下:

- Positive percent agreement (candidate method) = 100×a/(a+c)
- Negative percent agreement (candidate method) = 100×d/(b+d)
- Overall percent agreement = 100×(a+d)/n
从上可看出:
- Positive agreement is the proportion of comparative/reference method positive results in which the test method result is positive.
- Negative agreement is the proportion of comparative/reference method negative results in which the test method result is negative.
这里有几个注意点:
- PPA和NPA等一致性指标只能说明comparative和test的一致性比较好,但不能说明test的准确率(即跟金标准比)高,可能comparative和test准确率都不怎么好
- PPA是比较comparative方法阳性结果中,test方法结果也为阳性的比例
- 在使用时,可能还要注意目标人群患病率,有时候患病率的高低会影响到PPA和NPA;比如:假设test方法和comparative方法非常一致时,诊断的准确率是negative的;但当不一致率非常高时,诊断的准确率是positive的。那么在评估样本目标件患病率较低的研究中,两种方法之间的总体一致性会更高,而在评估样本目标患病率较高的研究中,这两种方法的总体一致性会更低。
那么如何计算PPA和NPA的置信区间CI呢,一般会使用Wilson方法来计算,可参考下述公式:
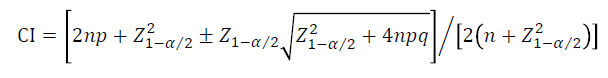
其中,PPA: p=a/(a+c), n=a+c, q=1-p
若不想根据函数写公式的话,可使用DescTools::BinomCI()函数,对于PPA,如:
DescTools::BinomCI(x = a, n = a+c, conf.level = 0.95, method = "wilson")除了wilson外,还可以建议用exact confidence limit(Clopper-Pearson)的方法,更改上述函数的参数即可:
DescTools::BinomCI(x = a, n = a+c, conf.level = 0.95, method = "clopper-pearson")以上大部分内容参考:CLSI EP12: User Protocol for Evaluation of Qualitative Test Performance,并只对其一部分内容做了笔记,若有理解上的偏差,请以原文为主
本文出自于http://www.bioinfo-scrounger.com转载请注明出处