以下内容参考EP09-A3和一些网上资料
平时研究工作中我们会用到最小二乘法的线性回归来做线性拟合;但是对于检测仪器(器械诊断领域)的方法学比较或者仪器间比较试,我们不仅要考虑Y所引入的随机误差,还需要考虑X所引入的随机误差,这时最小二乘法就不适用了,可以考虑用Deming回归
从EP09-A3中我们可以发现,一般是两种试剂/仪器的测量值的SD恒定时,首选Deming回归而不是OLR(最小二乘法的线性回归)
因此在实际Deming回归的使用中,还必须考虑X和Y方法对一组病人样品的检测值的分布是否一致,即要考虑每组x值的标准差Sx和y值的标准差Sy是否接近一致;还要考虑两个方法自身的重复精密度是否比较一致等,这个用于计算Deming回归中的lambda
从体外诊断试剂临床指导原则(征求意见稿)中可看出,一般OLR要求比较严格(要求因变量与自变量关系为线性、误差服从均数为0的正态分布且方差相等、各观测独立、X精确无误差(类似于金标准)等比较严格的条件),所以一般考虑Deming回归(Weighted Deming回归或者Passing-Bablock回归)
应根据数据分布特点等因素选择适用的回归分析方法,如Deming回归、Passing-Bablok回归分析和最小二乘回归估计等。其中最小二乘回归估计对数据的分布、等方差性等有较为严格的要求,可选用的情形较少。
在EP中还提到,对于具有非常宽的测量间隔的测量数据,SD很少是恒定的,反而可能存在比例关系;因此若数据满足比例差值是恒定的话,则可以用恒定CV Deming回归方法,即Weighted Deming回归;而且假如存在混合变化的,并且偏差图中在低浓度时未有明显的偏倚,则也可以用Weighted Deming回归
对于Deming和Weighted Deming的选择,可参考:
Use the Difference vs. Average plot and the residual plots to determine if the errors are constant and/or proportional. The choices are: * Simple Compute regular, unweighted Deming regression. This method should be used when the errors for the two variables are constant. * Weighted Compute weighted Deming regression. This should be used when the errors for the two methods are proportional but not necessarily constant.
以下根据mcr包的源码以及网上的资料,整理下 Weighted Deming(Deming回归类似,只需要在公式中去weight因子即可)的具体思路及公式
Weighted Deming回归算法原理:
设定初始变量:x, y, error.ratio(考核和对比的精密度比例,即CV的比例), iter.max(迭代次数), threshold(阈值)
根据下述公式计算初始b1(斜率),b0(截距),初始的w不做要求

- 根据下述公式计算X/Y的估计值及对应的weights
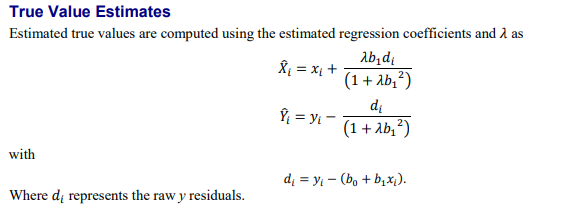
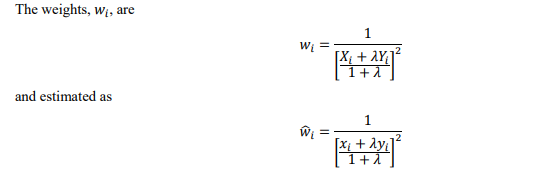
再次根据步骤2中公式估计Weighted Deming回归的B1(斜率估计值)和B0(截距估计值)
依次迭代步骤3-4,若步骤4中的B1与b1的绝对差值、B0和b0的绝对差值均小于阈值threshold,则迭代结束;或者迭代次数大于iter.max
得到回归方程最终的斜率和截距,然后通过jackknife计算估计值的置信区间
本文出自于http://www.bioinfo-scrounger.com转载请注明出处