我在maftools包的PlotOncogenicPathways函数分析了TCGA已知的10个致癌信号通路,统计了maf文件中在各个通路下的基因数目以及患者人数等信息
我发现数据集A在TGF-Beta通路中有5个基因发生突变,数据集B则有1个基因发生突变;我想知道这两个数据集(以某个指标区分开的)在TGF-Beta通路的基因突变比例是否有显著的统计学意义
主要参考:
http://www.sthda.com/english/wiki/comparing-proportions-in-r
后来想想由于数目太小,上述两者没有比较价值,就算是用Fisher检验也不太合适。。。但是总结下proportion test 相关知识点也算不错。。
One-Proportion Z-Test
One-Proportion Z-Test用于比较观测到的比例和理论比例是否有差别(具体看零假设)
Z统计量:
\[ z = \frac{p-p0}{\sqrt{p0(1-p0)/n}} \]
置信区间:
\[ p \pm 1.96\sqrt{\frac{pq}{n}} \]
Z统计量只有当样本数足够大(np/nq大于5,即当p为0.1时,n应当大于50)时才有效;因此当小样本时可以考虑使用exact binomial test
- binom.test(): compute exact binomial test. Recommended when sample size is small
- prop.test(): can be used when sample size is large ( N > 30). It uses a normal approximation to binomial
例如假设小鼠雌雄性格比为1:1(即0.5),而160只有自发性癌症的小鼠雄性95只,雌性65只,那么这癌症小鼠的性别比例是否正常呢?
首先利用公式计算,先计算Z统计量,然后计算显著性P值:
n <- 160
p0 <- 0.5
p <- 95 / 160
z <- (p - p0) / sqrt(p0 * (1 - p0) / n)
2 * pnorm(-abs(z))接着用binom.test()函数
binom.test(x = 95, n = 160, p = 0.5, alternative = "two.sided")以及prop.test()函数
prop.test(x = 95, n = 160, p = 0.5, correct = F, alternative = "two.sided")Two-Proportions Z-Test
Two-Proportions Z-Test 用于比较两个观测比例是否有差别
Z统计量:
\[ z = \frac{p_A-p_B}{\sqrt{pq/n_A+pq/n_B}} \]
如果样本数较少时(比如Z统计量需要满足np大于5),可以使用Fisher Exact Test(非参方法)
假如组A肺癌患者有500人,其中吸烟490人;组B健康个体有500人,其中吸烟400人;那么吸烟比例在两组人群中是否一样(即有无统计显著性差别)
计算过程:
n1 <- 500
p1 <- 400 / 500
n2 <- 500
p2 <- 490 / 500
p <- (p1 * n1 + p2 * n2) / (n1 + n2)
z <- (p1 - p2) / sqrt(p * (1 - p) * (1 / n1 + 1 / n2))
2 * pnorm(-abs(z))或者用prop.test()函数计算显著性
prop.test(x = c(400, 490), n = c(500, 500), correct = F, alternative = "two.sided")或者用Fisher Test的函数fisher.test()
fisher.test(matrix(c(490, 10, 400, 100), byrow = T, nrow = 2))Chi-square Goodness of Fit Test
Chi-square Goodness of Fit Test就我而言用的比较少,其主要用于比较多个观测比例与预期(理论)比例是否存在差异
例如假设你在某地区收集了野生郁金香,其中81朵是红色,50朵是黄色,27朵是白色;而该地区的野生郁金香各个颜色的预期(理论)比例分别是红色1/2,黄色1/3,白色1/6;那么你收集的观测数据与预期的数据是否有差别呢
chisq.test(c(81, 50, 27), p = c(1/2, 1/3, 1/6))Chi-Square Test of Independence
Chi-Square Test of Independence常用于分析列联表(contengency table),在临床上尤为常见,一般叫做卡方分析,用来判断两个分类变量之间是否有显著相关性(比如某基因突变是否与癌症是否相关等等),可用于计算OR值
有时样本量比较少时,一般会用Fisher精确检验来替代卡方检验
Chi-square test should only be applied when the expected frequency of any cell is at least 5.
这个卡方检验比较好理解,在教程中我比较感兴趣几种对于列联表可视化的方法,可以快速的展示数据
用gplots包的balloonplot()函数以气泡矩阵图形式展示数据,每个点代表数值的大小
library(gplots)
housetasks <- read.delim("http://www.sthda.com/sthda/RDoc/data/housetasks.txt", row.names = 1)
dt <- as.table(as.matrix(housetasks))
balloonplot(t(dt), main ="housetasks", xlab ="", ylab="",
label = FALSE, show.margins = FALSE)
用garphics包的mosaicplot()函数以堆砌直方图的形式展示数据
library(graphics)
mosaicplot(dt, shade = TRUE, las=2,
main = "housetasks")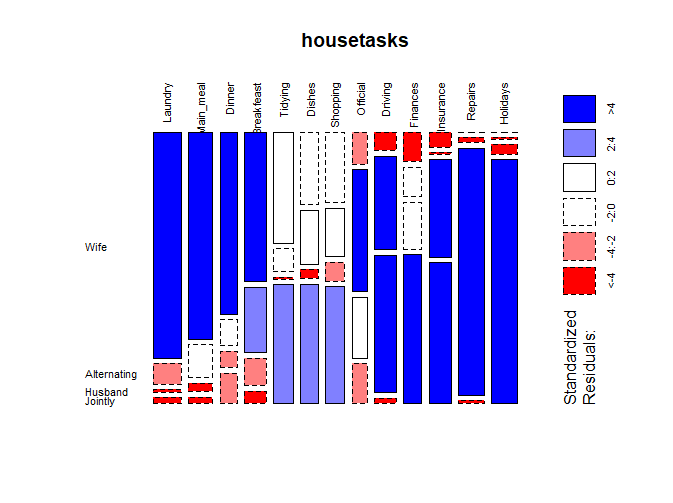
用vcd包的assoc()函数以马赛克图的形式展示数据
library(vcd)
# plot just a subset of the table
assoc(head(dt, 5), shade = TRUE, las=3)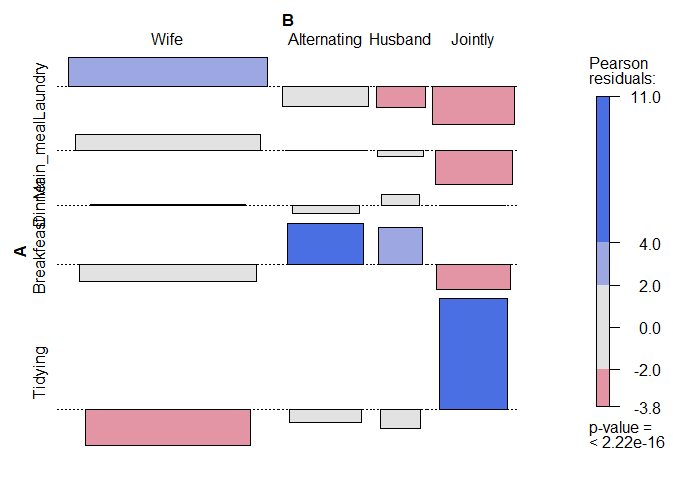
不知道是工作需要问题还是学校那会没好好上课,总感觉网上的教程比教科书那些例子更加通俗易懂,再加上有了编程代码后,再也不用再查表计算显著性P值了(也忘记怎么查了。。。)
参考资料
http://www.sthda.com/english/wiki/comparing-proportions-in-r
本文出自于http://www.bioinfo-scrounger.com转载请注明出处