在生物信息分析中,有时会看下基因突变之间是否会表现出mutual exclusion或者co-occurrence模式
在R中可以用maftools包的somaticInteractions()函数即可分析,如下所示
library(maftools)
laml.maf = system.file('extdata', 'tcga_laml.maf.gz', package = 'maftools')
laml.clin = system.file('extdata', 'tcga_laml_annot.tsv', package = 'maftools')
laml = read.maf(maf = laml.maf, clinicalData = laml.clin)
ss <- somaticInteractions(maf = laml, top = 25, pvalue = c(0.05, 0.01))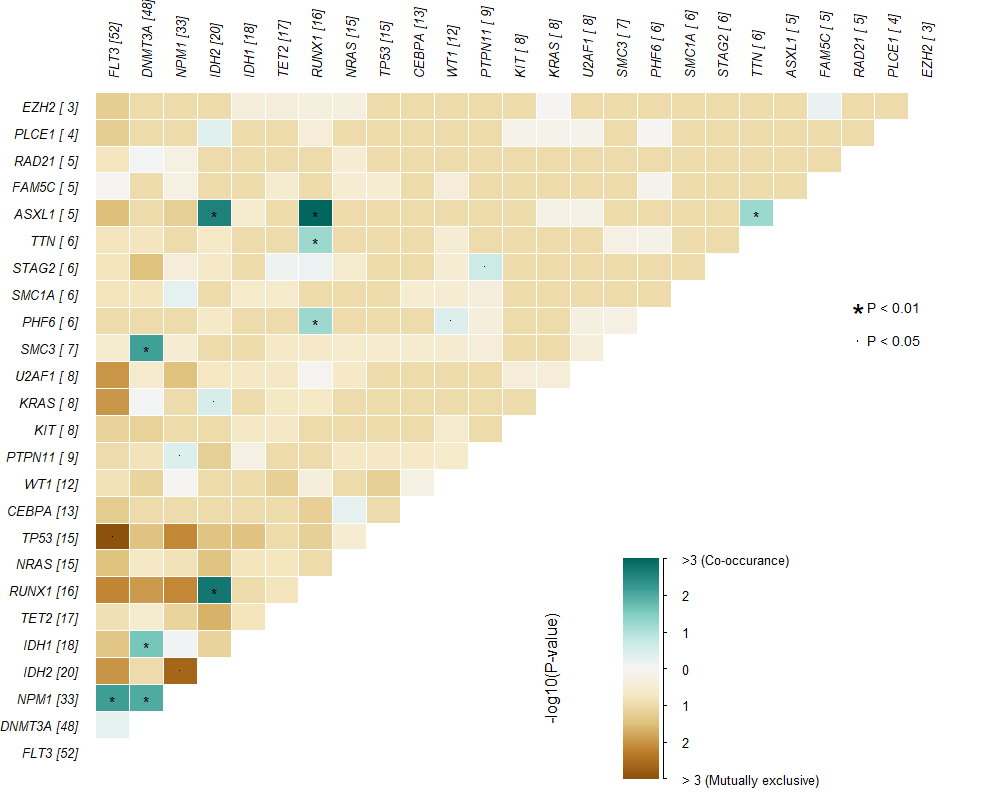
PS. 上述结果图中颜色展示略微有点问题,需要改下somaticInteractions的源码
按照作者所提示的,其是参考了NC的一篇文章中的方法:Combining gene mutation with gene expression data improves outcome prediction in myelodysplastic syndromes
在这篇文章中,作者通过odds ratio来区分co-mutation和 mutual exclusivity;对于OR值的计算,我们通常可以用Fisher’s Exact Test或者logistic regression来计算,可参考:Calculate odds ratio(OR) in R
从maftools包的函数源码可看出,作者采用的是Fisher’s Exact Test方法;从此角度来看,当OR值大于1时,说明两者(基因突变)呈正相关,即在其中的一个基因的突变先验假设下,另外一个基因突变频率变高了,当OR值小于1时,则反之,呈负相关;并通过P值来判断相关性的强弱,一般会选择0.05或者0.01进行过滤假阳性
比如我们先看下上述的结果数据
> head(ss)
gene1 gene2 pValue oddsRatio 00 11 01 10 Event pair event_ratio
1: ASXL1 RUNX1 0.0001541586 55.215541 176 4 12 1 Co_Occurence ASXL1, RUNX1 4/13
2: IDH2 RUNX1 0.0002809928 9.590877 164 7 9 13 Co_Occurence IDH2, RUNX1 7/22
3: IDH2 ASXL1 0.0004030636 41.077327 172 4 1 16 Co_Occurence ASXL1, IDH2 4/17
4: FLT3 NPM1 0.0009929836 3.763161 125 17 16 35 Co_Occurence FLT3, NPM1 17/51
5: SMC3 DNMT3A 0.0010451985 20.177713 144 6 42 1 Co_Occurence DNMT3A, SMC3 6/43
6: DNMT3A NPM1 0.0014582861 3.733141 128 16 17 32 Co_Occurence DNMT3A, NPM1 16/49结果中的00/11/01/10分别对应的四格表中的值,我们用fisher.test()看下结果是不是跟表中的oddsRatio值一样,以IDH2和RUNX1这对基因为例
dd <- matrix(c(7, 9, 13, 164), nrow = 2, ncol = 2)
> fisher.test(dd)
Fisher's Exact Test for Count Data
data: dd
p-value = 0.000281
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
2.598247 34.847384
sample estimates:
odds ratio
9.590877 如上所述,结果完全一致
一般到这就结束了,但是我将此方法应用到我的数据集中时发现,有很多基因之间呈现co-occurrence的模式(P值也小于0.05),仔细想想应该不至于会这样,因此怀疑还是有不少假阳性
有篇文章(Co-mutation and exclusion analysis in human tumors, a means for cancer biology studies and treatment design)提到,其觉得不少基因的突变频率其实很低的,因此突变率很低的基因会显得跟其他基因有co-occurrence模式,并且在Fisher Exact Test结果中通过假设检验
作者采用了计算二项比例分布的置信区间方式来过滤这些假阳性结果,思路如下:
- 计算observed联合突变概率及99%置信区间,这里的observed我理解为实际的共同突变比例
- 计算expected联合突变概率,这里的expected我理解为理论的共同突变比例
- 假如expected联合突变概率处于observed联合突变概率的99%置信区间内,则过滤去除
原文如下:
To filter this kind of false positives, we estimated the 99% confidence interval of each observed joint mutational probability and located the expected joint mutational probability. If the expected fell within the confidence interval of the observed, the pair was discarded, which is equivalent to filter all the dots near to the diagonal in the figure 1.
还是以IDH2和RUNX1这对基因为例:
计算observed概率的置信区间,其值为[0.0142, 0.0891]
> DescTools::BinomCI(7, 193, conf.level = 0.99)
est lwr.ci upr.ci
[1,] 0.03626943 0.01427524 0.08908793而expected概率为16/193=0.0829,其值在[0.0142, 0.0891]置信区间内,因此会被过滤。。。
置信区间的一些特点:
1.在样本量相同的情况下,置信水平越高,置信区间越宽,同样的样本取置信水平0.9、0.95、0.99,则置信区间的宽度有这样的关系,CI(0.9)<CI(0.95)<CI(0.99),CI为Confidence Interval简写。这很好理解,你希望估计的信心越大,你就要把区间取得越宽。
2.在置信水平相同的条件下,样本量越大,置信区间越窄。这也很好理解,以均值的置信区间为例,决定置信区间宽度的是方差,而决定样本均值的方差与样本量成反比,即样本量越大,样本均值的方差越小。
该篇文章的作者会对mutual exclusion以及co-occurrence模式做了分类(具体计算方式可看原文,主要比较条件概率与置信区间之间的大小):
If P(mi|mj) < CI(mi) AND P(mj|mi) < CI(mi) → mutual exclusion
If P(mi|mj) > CI(mi) AND P(mj|mi) > CI(mj) →bidirectional co-mutation

本文出自于http://www.bioinfo-scrounger.com转载请注明出处