Interaction revisited: the difference between two estimates

这篇文章有意思的地方在于其通过我们熟知的比较两个估计值的方法，推导出比较两个relative risks（或者odds ratios）的计算方法计算过程如下:

先获得两个Group组的RR值和95% CI for RR，并对两者都取log（95% CI有上下限范围，即两有个值）
计算上述两个Group的CI值的差值
可从95% CI值推导出SE（standard errors），SE[=width/(2×1.96)]
有了SE后，就可以计算两个log(RR)的差值d
然后通过假设检验计算统计量Z，从而得出P值
还可以计算差值的置信区间：CI(d)以及Ratio of relative risks (RRR)：exp(d)

具体示例可见文章中的示例图：

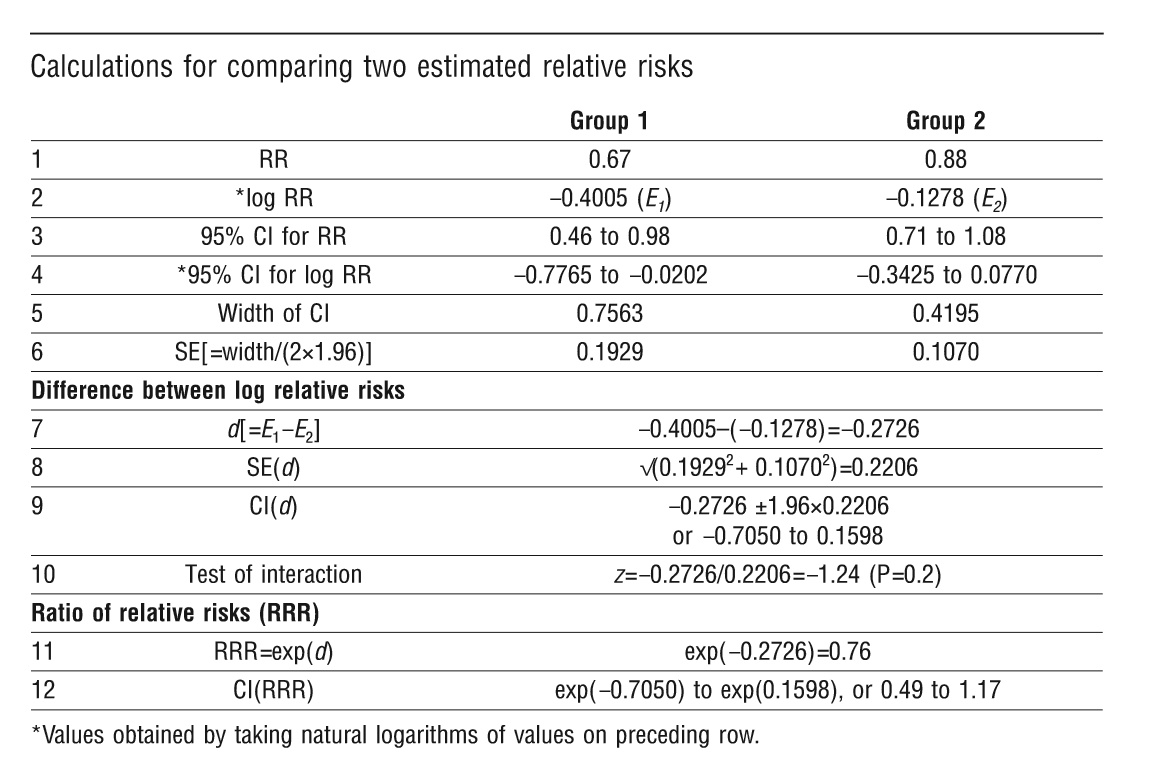
我以Cox回归计算出来的HR值为例，计算过程的R函数如下（g1/g2分别代表两个组，HR为风险比，upperCI/lowerCI分别为95% CI的上下限值）：

cal_p <- function(g1_HR, g1_upperCI, g1_lowerCI, g2_HR, g2_upperCI, g2_lowerCI){
  E1 <- log(g1_HR)
  E2 <- log(g2_HR)
  width_CI1 <- log(g1_upperCI) - log(g1_lowerCI)
  width_CI2 <- log(g2_upperCI) - log(g2_lowerCI)
  SE1 <- width_CI1 / (2 * 1.96)
  SE2 <- width_CI2 / (2 * 1.96)

  d <- E1 - E2
  d_SE <- sqrt(SE1^2 + SE2^2)
  Z <- d / d_SE
  p <- 2 * pnorm(-abs(Z))

  return(p)
}

本文出自于http://www.bioinfo-scrounger.com转载请注明出处