支持向量机(support vector machines, SVM)是一种二类分类模型,其很好的解决了感知机中模型有多解的问题,其基本模型是定义在特征空间上的间隔最大的线性模型
从历史上来讲SVM可谓是无人不知,但我第一次了解其是在一篇用SVM来在血液RNA表达数据中寻找生物标志物的文献(尴尬。。。),当时由于一连串看不懂的SVM术语,使我放弃了那篇文献方法部分的阅读。。。由于最近想从头开始了解下机器学习的一点知识,所以决定好好梳理下SVM实现的基本思路,了解其使用条件以及应用场景,不然可能连基本的调参都看不懂。。。下面是我摘抄的笔记(主要结合《统计学习方法》以及各个博客文章),不涉及公式推导(可参照网上大神们的资料),最后以代码形式整理下SVM的思路 SVM有其深厚的数学理论基础(从N个公式推导可看出),根据其应用的范围,从简至繁可以分为三部分(虽然三者的名字差不多,但是其应用的前提条件不一样,可以认为简单的模型是复杂模型的一种特殊情况,真是集大成者啊):
- 线性可分支持向量机
- 线性支持向量机
- 非线性支持向量机
线性可分支持向量机
线性可分支持向量机,从其名字中可看出,其前提条件是训练集线性可分,这点跟感知机一样;但感知机利用了误分类最小的策略,而这会使得分离超平面有无穷多个解;所以线性可分SVM做了改进,其利用了间隔最大化策略来寻找最优的分离超平面,即考虑了点到超平面的距离
距离的话会涉及两个概念:函数间隔和几何间隔,后者在前者的基础上对法向量w加了约束:规范化||w||,使得间距不会随着w和b的成比例变化而改变
进而使得我们可以根据几何间距,将一些离超平面最近的难分离点有效的区分开,即对一个训练点的分类,当超平面离训练点的几何间距越大,其分类的确信度也就越高
求解最大间隔分离超平面可以表示为有约束条件的最优化问题,最终求出w和b后,得到决策函数f(x)=sign(w*x+b),即线性可分SVM
从上可以引出一个概念,在线性可分的情况下,训练点中与分离超平面距离最近的样本点的实例叫支持向量,而这些支持向量也刚好间隔边界w*x+b=1或w*x+b=-1上;所以我们可以理解支持向量在决定分离超平面中起着决定性的作用,这也是支持向量机名字的来源
跟感知机一样,线性可分SVM可通过对偶算法来求解 ,即通过拉格朗日对偶性,将原始问题(有约束条件的最优化问题)转化为对偶问题,然后求解对偶问题进而得出原始问题的最优解("避开"了约束条件),对于这块内容可以参照关于SVM数学细节逻辑的个人理解(二):从基本形式转化为对偶问题
因此线性可分SVM学习算法就变成了:通过构建拉格朗日函数,求解最优条件下的α,进而(只考虑α>0)得出w和b,最终得到分类决策函数(见公式7.30)
线性支持向量机
现实中线性可分的数据集毕竟是少数,所以有些问题是线性不可分,比如在数据集中出现一些噪音及异常点,这事SVM就提出了软间隔这个概念(相对上面线性可分SVM的硬间隔)
线性不可分意味着有某些点不满足函数间隔大于等于1的约束条件;解决办法就是在约束条件上加一个松弛变量ζ(即对每个样本点引入一个松弛变量,使得一些离群点允许出现在函数间距小于1,即最大间隔空间内),在目标函数上加一个惩罚参数C(C相当于离群点的权重,C值大,则对误分类点的惩罚就大,反之惩罚就小),最后目标函数最小化问题就变成了:使间距尽量大,同时误分类点的个数尽量小
再经过上述优化了,线性SVM的学习算法的目标函数没有发生变成,但是其约束条件的最优解从αi>=0变成了0<=αi<=C,求出α后即可根据公式(7.50和7.51)求出w和b,最后得到分类决策函数
在上述线性SVM对偶算法推导过程中,涉及了KKT条件这个概念真正理解拉格朗日乘子法和 KKT 条件;KKT条件在后面SVM算法实现的过程中用来判断一些样本点是否需要被优化(不满足KKT即需要被优化)
Python · SVM(四)· SMO 算法,这篇文章中对于KKT条件有个比较好的理解:
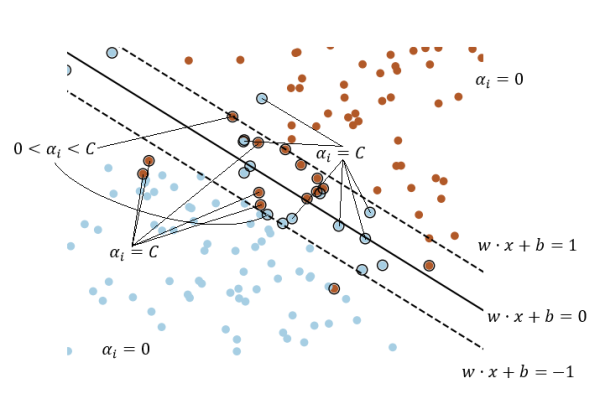
- αi=0 <=> 样本离间隔超平面比较远
- 0<αi 样本落在间隔超平面上
- αi=C <=> 样本在间隔超平面以内
这里有个注意的地方:满足ai>0的点是支持向量,其可以在间隔边界上,也可以在间隔边界与分离超平面之间,或者在分离超平面误分一侧
一个通俗易懂的图:
非线性支持向量机
支持向量机其实做到上面的层次,我觉得已经很NB了,毕竟其已经可以适用于线性不可分的情况,但是其又有进一步的优化,即非线性支持向量机,毕竟现实中非线性问题是一个普遍的现象,这也是为什么其能广泛应用的原因之一吧(我觉得。。)
其为了解决非线性问题,引用了核函数这个概念:即用核函数将非线性原始数据映射到另一个线性的空间内,而且SVM的目标函数中刚好有适用于这核函数的地方。。。是很巧(数学家真NB。。。)
常用的核函数有:线性核、多项式核、高斯核、拉普拉斯核、sigmoid核等,因此对于不同核函数的选择会导致最终的结果的不同
最后则是非线性SVM学习算法的最优化算法,即SMO算法,这部分也是我花了最多时间理解的部分,最终思路都在后面的代码中了,一些理论说明可以看机器学习算法与Python实践之(四)支持向量机(SVM)实现
SM算法简单的说是:每次迭代只选出两个变量,即ai和aj进行调整,其它变量保持不变,在得到解αi和αj之后,再用αi和αj改进其它分量,从而达到通过分次获得最优α值
综上所述SVM的Python代码实现如下(相当于将SOM算法的公式用代码表述出来),其中kernelMatrix是所有样本点的核函数矩阵,E则是样本i的SVM输出和预期的差:
class SVM:
def __init__(self, X, y, sigma = 10, C = 200, toler = 0.001):
self.X = X
self.y = np.ravel(y)
self.numSamples = X.shape[0]
self.sigma = sigma # 高斯核函数的sigma参数
self.C = C # 惩罚参数
self.toler = toler # 松弛变量
self.b = 0 # 偏置b
self.alphas = np.zeros(self.X.shape[0]) # 储存α的数组
self.E = np.zeros(self.X.shape[0]) # 储存E的数组
self.kernelMatrix = self.calc_Kernel() # 储存核函数值的矩阵
# 根据公式7.66和7.90计算高斯核
def calc_Kernel(self):
k_matrix = np.mat(np.zeros((self.numSamples, self.numSamples)))
for i in range(self.numSamples):
x = self.X[i,:]
for j in range(i, self.numSamples):
z = self.X[j,:]
r = (x - z) * (x - z).T
gsi = np.exp(-1 * r / (2 * self.sigma ** 2))
k_matrix[i,j] = gsi
k_matrix[j,i] = gsi
return k_matrix
# 根据公式7.104和7.105计算
def calc_E(self, i):
gx = np.multiply(self.alphas, self.y) * self.kernelMatrix[:,i] + self.b
Ei = gx - self.y[i]
return Ei
# 选择变量2,采用|E2-E1|最大原则
def select_AlphaJ(self, i, E1):
E2 = 0
maxE1_E2 = -1
maxIndex = -1
# 只看E>0的
nozeroE = [i for i, Ei in enumerate(self.E) if Ei != 0]
if (len(nozeroE) > 0):
for j in nozeroE:
if j == i: continue
Ej = self.calc_E(j)
if math.fabs(E1 - Ej) > maxE1_E2:
maxE1_E2 = math.fabs(E1 - Ej)
E2 = Ej
maxIndex = j
else:
maxIndex = i
while maxIndex == i:
maxIndex = int(random.uniform(0, self.numSamples))
E2 = self.calc_E(maxIndex)
return maxIndex, E2
# 先外循环找变量1再内循环找变量2
def Loop(self, i):
E1 = self.calc_E(i)
# 寻找不满足KKT条件的点,这里我也是学了他人的取巧方式,具体推理可看上面那篇文章
if (self.y[i] * E1 < -self.toler and self.alphas[i] < self.C) or (self.y[i] * E1 > self.toler and self.alphas[i] > 0):
j,E2 = self.select_AlphaJ(i, E1)
alpha_old_1 = self.alphas[i]
alpha_old_2 = self.alphas[j]
y1 = self.y[i]
y2 = self.y[j]
# 有图7.8所得
if y1 != y2:
L = max(0, alpha_old_2 - alpha_old_1)
H = min(self.C, self.C + alpha_old_2 - alpha_old_1)
else:
L = max(0, alpha_old_2 + alpha_old_1 - self.C)
H = min(self.C, alpha_old_2 + alpha_old_1)
# 说明无法再优化
if L == H:
return 0
# 公式7.106 7.107
alpha_new_2 = alpha_old_2 + y2 * (E1 - E2) / (self.kernelMatrix[i,i] + self.kernelMatrix[j,j] - 2 * self.kernelMatrix[i,j])
# 公式7.108
if (alpha_new_2 > H):
alpha_new_2 = H
elif (alpha_new_2 < L):
alpha_new_2 = L
# 公式7.109
alpha_new_1 = alpha_old_1 + y1 * y2 * (alpha_old_2 - alpha_new_2)
# 公式7.115 7.116
b1_new = -1 * E1 - y1 * self.kernelMatrix[i,i] * (alpha_new_1 - alpha_old_1) - y2 * self.kernelMatrix[j,i] * (alpha_new_2 - alpha_old_2) + self.b
b2_new = -1 * E2 - y1 * self.kernelMatrix[i,j] * (alpha_new_1 - alpha_old_1) - y2 * self.kernelMatrix[j,j] * (alpha_new_2 - alpha_old_2) + self.b
if (alpha_new_1 > 0) and (alpha_new_1 < self.C):
b_new = b1_new
elif (alpha_new_2 > 0) and (alpha_new_2 < self.C):
b_new = b2_new
else:
b_new = (b1_new + b2_new) / 2
# 更新a1 a2以及E1 E2
self.alphas[i] = alpha_new_1
self.alphas[j] = alpha_new_2
self.b = b_new
self.E[i] = self.calc_E(i)
self.E[j] = self.calc_E(j)
if (math.fabs(alpha_new_2 - alpha_old_2) < 0.00001):
return 0
else:
return 1
else:
return 0
def train(self, max_iter = 1000):
alpha_change = 1
iter = 0
entireSet = True
while (iter < max_iter) and (alpha_change > 0) or entireSet:
alpha_change = 0
iter += 1
# 先过一遍全部样本,然后就先支持向量的样本,都满足的KKT的话,再全样本
if entireSet:
for i in range(self.numSamples):
alpha_change += self.Loop(i)
print("iter:", iter, "i value:", i, "entire_Set, alpha changed:", alpha_change, "b:", self.b)
else:
support_vector_i = [i for i, alpha in enumerate(self.alphas) if alpha > 0 * alpha < self.C]
for i in support_vector_i:
alpha_change += self.Loop(i)
print("iter:", iter, "i value:", i, "support_vector_Set, alpha changed:", alpha_change, "b:", self.b)
if entireSet:
entireSet = False
elif alpha_change == 0:
entireSet = True
#单个核函数计算函数,用于公式7.90
def calcKernelValue(self, xj, xi):
r = (xj - xi) * (xj - xi).T
gsi = np.exp(-1 * r / (2 * self.sigma ** 2))
return gsi
# 预测函数
def predict(self, test_X):
support_vector = np.nonzero(self.alphas > 0)[0]
gx = 0
for i in support_vector:
kernel_value = self.calcKernelValue(self.X[i,:], test_X)
gx += self.alphas[i] * self.y[i] * kernel_value
gx += self.b
return np.sign(gx)上述SVM实现方式我主要是参照网上资料统计学习方法|支持向量机(SVM)原理剖析及实现,前人写的是真好,对于我理解SVM算法帮助很大(因为单看公式的话容易看过就忘),接下来就是拿一个测试集(跟前一篇博文逻辑斯蒂回归一样的)来试试
import numpy as np
import pandas as pd
import math
import random
from sklearn.model_selection import train_test_split
dataset = pd.read_table("testSet.txt", header = None)
dataset = np.mat(dataset)
X = dataset[:,:-1]
y = dataset[:,-1]
y[y == 0] = -1
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size = 0.2, random_state = 123456)
svm = SVM(X=train_X, y=train_y, C=10)
svm.train()
error = 0
for i in range(test_X.shape[0]):
p = svm.predict(test_X[i])
if p != test_y[i]:
error += 1
print(error / len(test_y) * 100)测试误差为0%
以上的一些SVM是理解笔记,很浅的理解,但是用于SVM的简单实用是暂时够了,好歹让我明白了SVM的一些参数是怎么来的,干嘛用的了。。。
参考资料:
关于支持向量机(SVM)的原理,你了解多少?(万字长文 速收)
统计学习方法|支持向量机(SVM)原理剖析及实现
机器学习算法与Python实践之(四)支持向量机(SVM)实现
真正理解拉格朗日乘子法和 KKT 条件
关于SVM数学细节逻辑的个人理解(二):从基本形式转化为对偶问题
本文出自于http://www.bioinfo-scrounger.com转载请注明出处