KeepNotes blog

Stay hungry, Stay Foolish.

0%

PCA实现过程梳理以及降噪处理

Posted on Edited on In
Symbols count in article: 3.9k Reading time ≈ 4 mins.

现在CNV分析方法有很多，但是随着NGS成本的降低，高深度的测序下背景下，read count（depth）方法逐渐变为各个分析软件的主流。最近在看GATK的CNV分析方法，其中在创建PoN(PanelofNormals)和denoise过程都使用了PCA(Principal Component Analysis)的奇异值分解(Singular Value Decomposition, SVD)方法，因此有比较对PCA思路做个梳理以及了解下常见的如何使用PCA来降噪（denoise） R语言中，PCA一般常用的基础函数是prcomp和princomp，两者有些差别：

  • prcomp适用于R mode和Q mode，而princomp只适用于R mode
  • prcomp基于奇异值分解（SVD），求最小二乘的优化解（最小化的结果要求寻找一个正交矩阵AB,记作H[q]，H[q]为投影矩阵，把每个点X[i]投影到q维结构H[q]x[i],这是由V[q]的列限定的x[i]的正交投影）
  • princomp是基于相关系数矩阵的特征值分解，方差最大化方法（本质上是求原始变量协方差/相关系数矩阵的特征值和特征向量，第i主成分对应着协方差的第i大特征值，投影方向为该特征值对应的特征向量，而特征值等于相应主成分的方差，因此代表着对应主成分分解原始信息的多少）
  • prcomp在参数中如果设定了scale=T，那么如果princomp结果想与prcomp保持一致，则princomp函数需加上cor=T参数（其实原因在于cor和cov之间刚好相差了一个scale）

参考自使用R的统计学习：算法和实践（二）：PCA（1）

R mode是指基于variable分析，一般来研究variable之间的关系，当数据集的observation数目大于variable时；Q mode是指基于observation分析，一般来研究observation之间的的关系，当数据集的varibale数目大于observation时

从R代码的角度来实现下PCA实现思路（原理部分可以看图文并茂的PCA教程），并与prcomp函数的结果比较下，代码参考PRINCIPAL COMPONENTS ANALYSIS (PCA)；使用自带数据集USArrests作为测试对象

先是prcomp函数通过奇异值分解来实现PCA分析，res1$sdev是特征值的平方根（由矩阵的奇异值计算得出的），res1$rotation是变量的loading矩阵（每列是对应主成分的特征向量），res1$x是PCA projections ("scores")

data(USArrests)
dim(USArrests)

res1 <- prcomp(USArrests, scale = T)
sd <- res1$sdev
loadings <- res1$rotation
scores <- res1$x

然后是R代码实现

R <- cor(USArrests)

# find the eigenvalues and eigenvectors of correlation matrix
myEig <- eigen(R)

# eigenvalues stored in myEig$values
# eigenvectors (loadings) stored in myEig$vectors
loadingsLONG <- myEig$vectors
rownames(loadingsLONG) <- colnames(USArrests)

# calculating singular values from eigenvalues
sdLONG <- sqrt(myEig$values)

# transforming data to zero mean and unit variance
X <- apply(USArrests, 2, function(x){
  (x - mean(x))/sd(x)
})

# calculating scores from eigenanalysis results
scoresLONG <- X %*% loadingsLONG

比较两者的前后两种方法的差异（其实是很小的）

range(sd - sdLONG)
range(loadings - loadingsLONG)
range(scores - scoresLONG)

如果想降噪，则简单的说相当于要做了以下步骤：

下面用一个示例来说明下使用不同k维下的区别，用R代码来说明下如何进行降噪。参考一篇文章R Basics: PCA with R和帖子How to reverse PCA and reconstruct original variables from several principal components?以及How to perform dimensionality reduction with PCA in R

测试数据是Kaggle上的一个测试数据集MNIST

require(data.table)
mnist_data=fread('../Desktop/all/train.csv')

然后对数据进行预处理，去除掉对应的观测值是常量的变量（具体原因可看上述那篇文章）

mnist_data2 <- mnist_data[,-(which((1:784)%%28<=2|(1:784)%%28>=26|(1:784)%/%28<=2|(1:784)%/%28>=26)+1), with=F]

使用prcomp函数进行PCA分析，并从解释方差比例角度来看下不同主成分的重要性

pca_res <- prcomp(mnist_data2[,(2:ncol(mnist_data2)), with=F], center = T, scale. = F)
plot(cumsum(pca_res$sdev^2)/sum(pca_res$sdev^2)*100, 
 ylab = 'Cumulative proportion of variance explained', xlab = "Principal Component")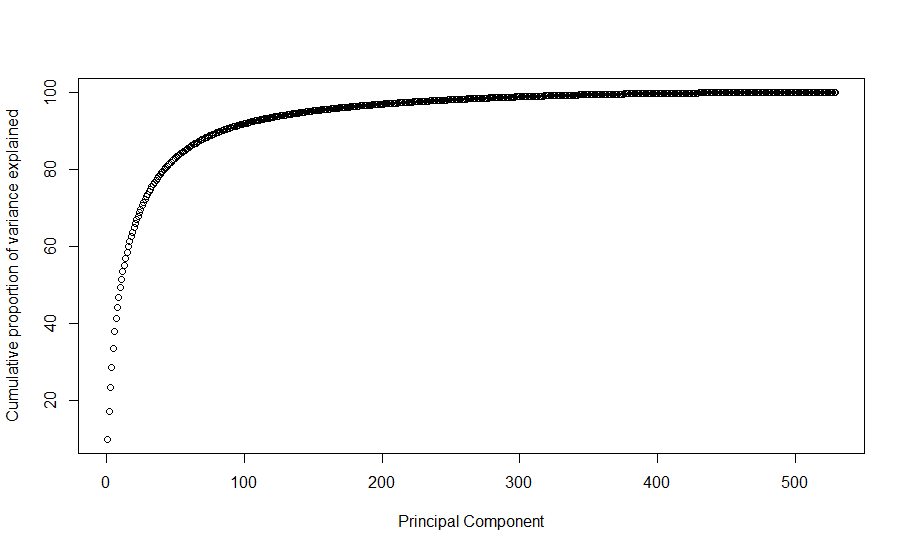
pca_denoise1

最后看下新投影（或者说reconstruct后的）数据集

pc_use <- 300
trunc <- pca_res$x[,1:pc_use] %*% t(pca_res$rotation[,1:pc_use])
trunc <- scale(trunc, center = -pca_res$center, scale = pca_res$scale)
dim(trunc)
res <- data.table(mnist_data2$label, trunc)

并与初始数据集的图片做个比较看下，原数据集如下：

par(mfrow=c(3,3))
for (i in 1:9) {
  ##Changing i-th row to matrix
  set.seed(123456)
  rad <- sample(which(mnist_data[,1] == i), 1)
  mat <- matrix(as.numeric(mnist_data[rad, 785:2]), nrow = 28, ncol = 28, byrow = F)
  ##Inverting row order
  mat <- mat[nrow(mat):1,]
  ##plot
  image(mat,main=paste0('This is a ', i))
}
pca_denoise2

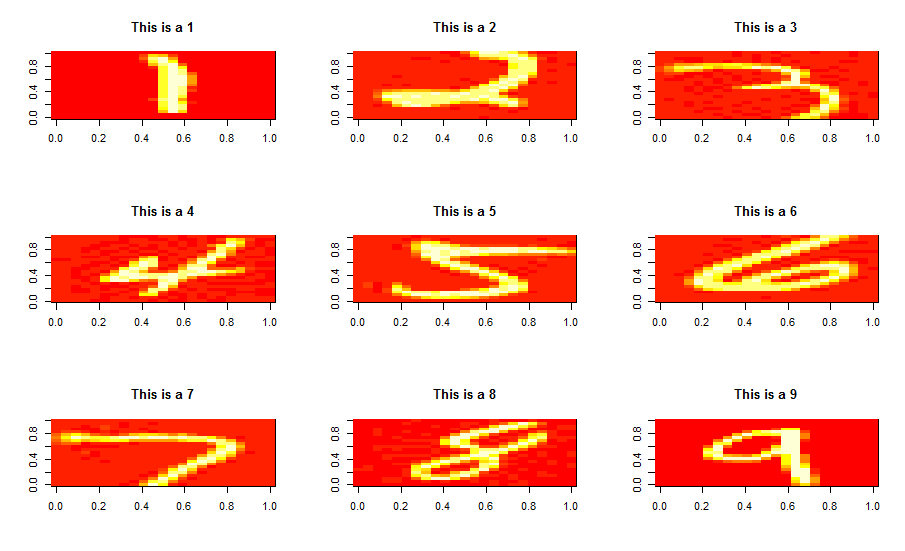
再看下只取前300个主成分的新投影数据集（其去除了不太重要的一些维度，降低了维度）

par(mfrow=c(3,3))
for (i in 1:9) {
  set.seed(123456)
  rad <- sample(which(res[,1] == i), 1)
  mat <- matrix(as.numeric(res[rad, 530:2]), nrow = 23, ncol = 23, byrow = F)
  mat <- mat[nrow(mat):1,]
  image(mat,main=paste0('This is a ', i))
}
pca_denoise3.png

从图像降噪的角度来看，上述的例子不太好，可以看这篇用Python来实现PCA降噪的文章机器学习：PCA（降噪），来实现对高斯噪声的去除

总之，使用PCA等手段可以有效的去除一些噪声，压缩等

其他参考文章：
Reversing PCA back to the original variables [duplicate]
http://statmath.wu.ac.at/~hornik/QFS1/principal_component-vignette.pdf
一篇深入剖析PCA的好文
R语言主成分分析——prcomp VS princomp
R语言主成分分析——prcomp VS princomp
初识R语言——PCA的实现

本文出自于http://www.bioinfo-scrounger.com转载请注明出处

Related Posts