这篇笔记连标题都懒得想了(照搬教程标题。。。),继续接上篇R语言-Cox比例风险模型和上上篇Survival analysis(生存分析) 先把我学习的教程放在最上面Cox Model Assumptions
这篇主要是讲述如何验证Cox回归模型的有效性,主要从三个方面:
- Testing the proportional hazards assumption(检验Cox比例风险模型的前提假设是否成立)
- Examining influential observations (or outliers)(检查是是否有异常值)
- Detecting nonlinearity in relationship between the log hazard and the covariates(检测风险与协变量之间的非线性关系)
Cox比例风险模型的前提是:在某因素下,个体的风险比例在不同时间点都是定值;只有满足这个前提,才能使用Cox回归模型;就像一些假设检验,需要数据总体满足正态分布才能使用一样;本文使用Schoenfeld残差来检验比例风险假设(还可以简单的通过生存曲线是否交叉来粗略判断下)
如果数据满足Cox回归模型,那么则Schoenfeld残差和生存时间的秩次之间无明显的相关性,也就是说Schoenfeld残差与生存时间无明显的一致变化趋势,这里通过survival包的cox.zph()函数即可判断
library("survival")
library("survminer")
res.cox <- coxph(Surv(time, status) ~ age + sex + wt.loss, data = lung)
test.ph <- cox.zph(res.cox)
> test.ph
rho chisq p
age -0.0483 0.378 0.538
sex 0.1265 2.349 0.125
wt.loss 0.0126 0.024 0.877
GLOBAL NA 2.846 0.416这里对年龄,性别以及体重减少这三个协变量做Cox回归,从test.ph结果中的三个协变量的P值可看出,检验均不显著,说明每个协变量均满足proportional hazards假设,而且模型总体(global)也不显著,因此可得出这Cox回归模型的前提是成立的
此外我们还可以通过Schoenfeld残差与时间的关系图来诊断模型是否满足前提,理论上如果满足的话,Schoenfeld残差应该与时间无明显的趋势,使用ggcoxzph函数,非常方便
ggcoxzph(test.ph)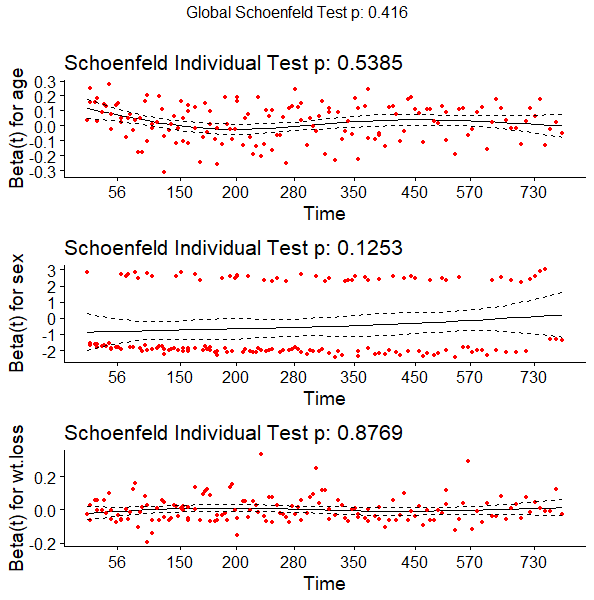
图中实线是散点的平滑拟合线,虚线则代表拟合线的正负两个标准差;从图中也很明显的看出三个协方差均满足proportional hazards假设(如果曲线偏离2个标准差则表示不满足比例风险假定)
如果是分类协变量,则还可以通过绘制log(-log(S(t)))与t(或者log(t))来看是否平行来判断是否满足Cox假设
如果不满足proportional hazards假设,则可以通过以下手段解决:
- Adding covariate*time interaction(增加协变量与时间的交互关系)
- Stratification(分层)
为了检测影响模型的点,或者说是异常值,我们可以通过展示deviance residuals或者dfbeta values图形来实现(也是一种残差图),主要使用ggcoxdiagnostics函数,type参数选择残差类型
ggcoxdiagnostics(res.cox, type = "dfbeta", linear.predictions = FALSE, ggtheme = theme_bw())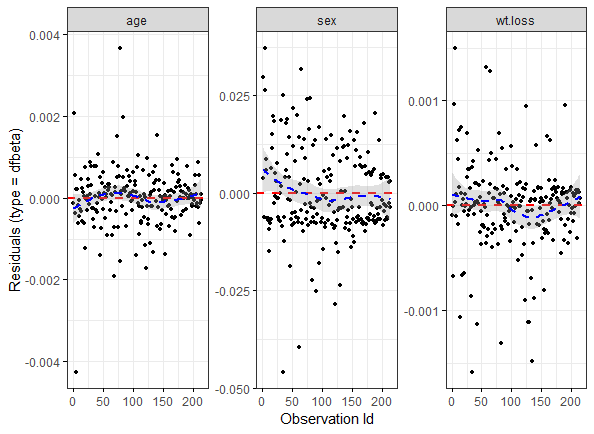
从上图可看出,尽管一些dfbeta值(相对于回归系数的)很大,但是都不影响模型的估计值
我们还可以通过deviance残差图来检查异常值
ggcoxdiagnostics(res.cox, type = "deviance", linear.predictions = FALSE, ggtheme = theme_bw())
deviance残差一般以标准差为1对称分布在0附近,如果:
Deviance残差如果大于0,提示预测结局发生的时间比实际结局发生的时间少,即风险率会高估。如果Deviance残差小于0,则提示预测结局发生的时间比实际结局发生的时间长,即风险率会低估。得分残差显示了删除某个观测后模型中系数变化的大小,变化越大,表示该观测对模型的影响越大。如果模型中很多观测的残差都较大,提示模型拟合的可能有问题
一般来说我们都假设连续协变量是呈线性的,通过绘制Martingale残差与协变量的散点图来检验非线性
Martingale残差范围一般在(-INF,1),如果其值接近于1则说明预测结局发生的时间比实际结局发生的时间少,即风险率会高估(died too soon);如果其值是极小的负值则说明预测结局发生的时间比实际结局发生的时间长,即风险率会低估(lived too long)
为了评估连续协变量的拟合形式,符合线性拟合形式的话则说明满足Cox模型的假设,可以用ggcoxfunctional()函数来查看协变量和martingale残差的分布情况
res.cox <- coxph(Surv(time, status) ~ age + log(age) + sqrt(age), data = lung)
ggcoxfunctional(res.cox, data = lung, point.col = "blue", point.alpha = 0.5)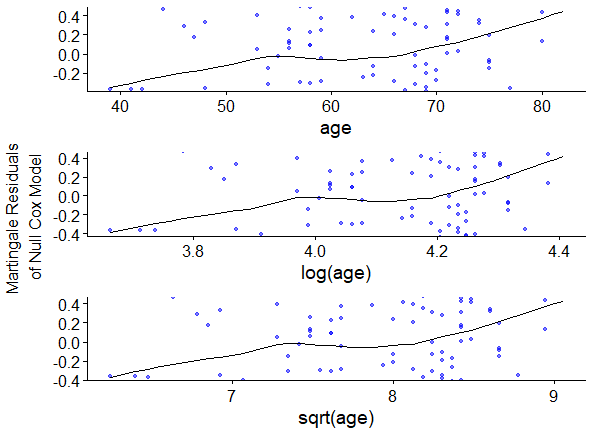
从图中可看出有略微非线性,但是整体还是有线性趋势的
参考资料:
Cox Model Assumptions
生存分析函数小结
基于R语言实现COX模型诊断
关于cox回归
本文出自于http://www.bioinfo-scrounger.com转载请注明出处