R语言 PCA分析

PCA（Principal Components Analysis）即主成分分析，一种无监督算法，降维中的最常见的一种方法

为什么要降维：

减少高维数据的处理难度，降低后续计算的复杂度
去除噪音和冗余数据，同时减少信息的损失
低维数据相比高维更加容易理解及可视化

PCA的本质：将具有相关性的高维变量通过线性变换投影到低维空间上，这低维变量称为主成分；并且通过最大方差理论使得第一主成分能对原始数据更多的解释（变异最大，也就是方差最大），同时也使得这些低维度变量的相关尽可能的小，便于后续分析 > 在空间上，PCA可以理解为把原始数据投射到一个新的坐标系统，第一主成分为第一坐标轴，它的含义代表了原始数据中多个变量经过某种变换得到的新变量的变化区间；第二成分为第二坐标轴，代表了原始数据中多个变量经过某种变换得到的第二个新变量的变化区间，并且保持与前一个主成分正交，仅次于前一个主成分的最大方差。

PCA usage

所以PCA是一种无监督算法，也就是我们不需要标签也能对数据做降维；但是降维后，我们则无法理解每个维的含义，也就是脱离了那些标签，从而使得对数据更加难理解了；当然至少减少了数据维度，使得计算机能更好的识别

从而可以简单的说，PCA把原来高维的数据（多个特征）用低维（少量特征值）来代替，新的维度是原先高维度的线性组合，这些组合变量（方差最大）尽可能代表原来的变量，而且彼此之间互不相关，因此对于一些冗余的数据有很好的表现

PCA的原理参看：
主成分分析（PCA）一次讲个够

原理不细说了，因为自身也只是勉强看懂，只要记住其核心在于协方差矩阵，求解特征值和特征向量，最终变换成新的主成分矩阵即可

因此我们可以通过PCA方法对一些样本进行分类，比如我们有一些组学（NGS转录组/蛋白组/代谢组）的表达谱数据，这里每个基因/蛋白/代谢物都是一个变量，如果我想用将所有变量来表示样本的分类是不现实的，每个表达谱都会涉及上万个基因/上千个蛋白/上百个代谢物，所以我要从中找出最具代表性的主成分来对样本进行区分

除了上述组学数据，还有一些芯片数据，如转录芯片以及甲基化芯片均可用其值来做PCA

对于以上组学数据来说，样本是观测值，也就是指标，基因等数据则是变量；我们需要通过较少的变量来代替这些样本，从而能在较低维度可视化样本的分布，因此我们常常能看到PCA在组学数据中用来看看不同组样本之间的分布情况，看看有无离群样本以及样本变化情况

那么如何用R来实现PCA分析呢

结合PCA - Principal Component Analysis Essentials的教程（非常棒的教程，有事没事都可以去翻翻看看）及测试数据来做个简单的整理

测试数据

factoextra包的decathlon2的数据集，收集了运动员的一些比赛的表现，取其有效部分作为后续PCA分析的数据
```
library("FactoMineR")
library("factoextra")

data(decathlon2)
data <- decathlon2[1:23, 1:10]
```
数据标准化

如果变量之间的数据的处于不同数量级或者变量之间的均值/方差相差很大时，建议是进行标准化的，PCA降维之前为什么要先标准化

常见的用scale()函数，输入矩阵，以列（列名是变量）进行标准化；如果是用FactoMineR包的PCA()函数的话，自带标准化参数(其实基础包的prcomp()函数也自带)，如下：
```
library("FactoMineR")
res.pca <- PCA(data, graph = FALSE)
```
PCA数据分析

PCA结果分析及可视化首推factoextra包，能处理各种R函数计算PCA的结果，有：

stats::prcomp()
FactoMiner::PCA()
ade4::dudi.pca()
ExPosition::epPCA()

如果我们想判断PCA中需要多少个主成分比较好，那么可以从主成分的特征值来考虑（Kaiser-Harris准则建议保留特征值大于1的主成分）；特征值表示主成分所保留的变异量（所解释的方差）；如用get_eigenvalue函来提取特征值，结果中第一列是特征值，第二列是可解释变异的比例，第三列是累计可解释变异的比例
```
> eig.val <- get_eigenvalue(res.pca)
> eig.val
       eigenvalue variance.percent cumulative.variance.percent
Dim.1   4.1242133        41.242133                    41.24213
Dim.2   1.8385309        18.385309                    59.62744
Dim.3   1.2391403        12.391403                    72.01885
Dim.4   0.8194402         8.194402                    80.21325
Dim.5   0.7015528         7.015528                    87.22878
Dim.6   0.4228828         4.228828                    91.45760
Dim.7   0.3025817         3.025817                    94.48342
Dim.8   0.2744700         2.744700                    97.22812
Dim.9   0.1552169         1.552169                    98.78029
Dim.10  0.1219710         1.219710                   100.00000
```
除了卡特征值大于1作为主成分个数的阈值外，还可以设置总变异的阈值（累计）作为判断指标

除了看表格来判断，还可从图形上直观的感受下
```
fviz_eig(res.pca, addlabels = TRUE, ylim = c(0, 50))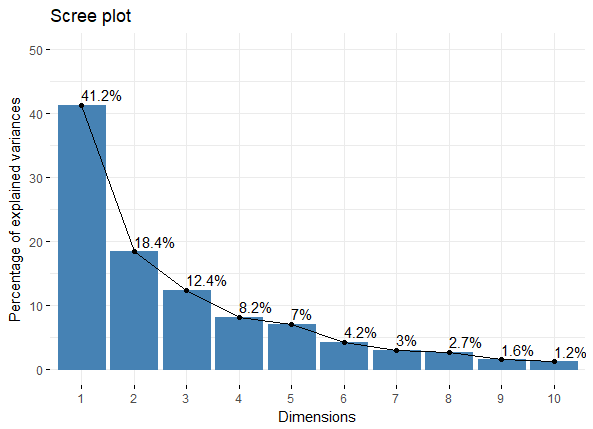
```
fviz_eig_PCA_plot

如果我们想提取PCA结果中变量的信息，则可用get_pca_var()
```
var <- get_pca_var(res.pca)
```
比如我们用于展示变量与主成分之间的关系，以及变量之间的关联，可直接用head(var$coord)查看，或者图形展示
```
fviz_pca_var(res.pca, col.var = "black")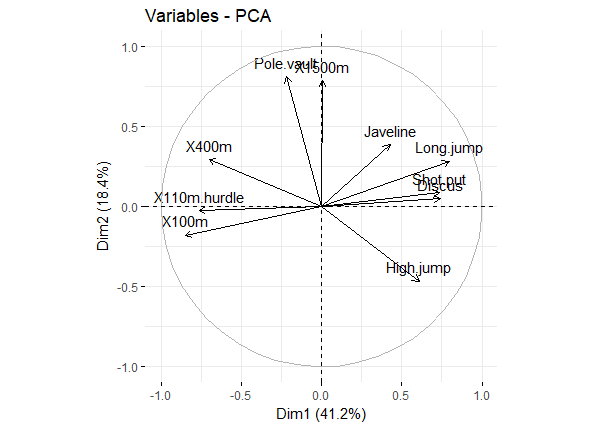
```
pca_var_corrd

图形解释，见原文吧：
- Positively correlated variables are grouped together.
- Negatively correlated variables are positioned on opposite sides of the plot origin (opposed quadrants).
- The distance between variables and the origin measures the quality of the variables on the factor map. Variables that are away from the origin are well represented on the factor map
除了上面的Correlation circle外，还有Quality of representation（对应var$cos2），用于展示每个变量在各个主成分中的代表性（高cos2值说明该变量在主成分中有good representation，对应在Correlation circle图上则是接近圆周边上；低cos2值说明该变量不能很好的代表该主成分，对应Correlation circle图的圆心位置）；对于变量来说，所有主成分上cos2值的和等于1，所以变量在越少主成分下累计cos2值接近于1，则其在Correlation circle上处于圆周圈上
```
library("corrplot")
corrplot(var$cos2, is.corr=FALSE)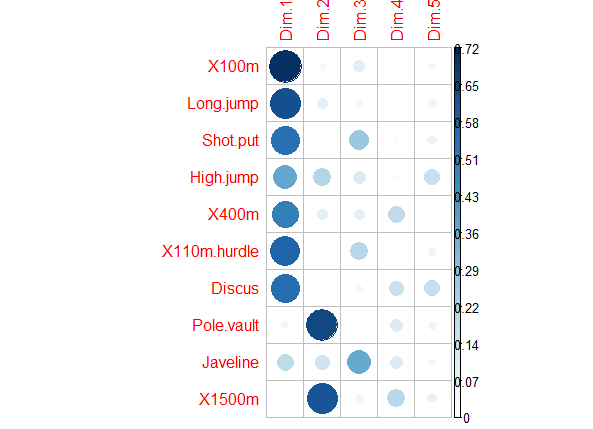
```
pca_var_cos2

对于cos2值的原文总结：
- The cos2 values are used to estimate the quality of the representation
- The closer a variable is to the circle of correlations, the better its representation on the factor map (and the more important it is to interpret these components)
- Variables that are closed to the center of the plot are less important for the first components.
针对上述的cos2值，还有一个与其相关的则是Contributions to the principal components，也就是cos2值在各个主成分中的比例。。

简单的说，如果一个变量在PC1和PC2的Contributions很高的话，则说明该变量可有效解释数据的变异，我们可以用图形展示各个变量在PC1和PC2上的Contributions
```
fviz_pca_var(res.pca, col.var = "contrib",
     gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07")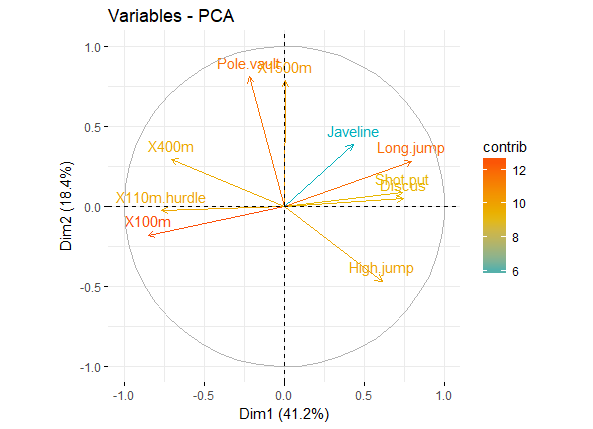
     )
```
pca_var_contrib

以上均是对变量在PCA中的分析，下面则是观测值的分析

跟上述变量的分析一样，先用提取出individuals信息，会发现也有coord，cos2和contrib等信息
```
> ind <- get_pca_ind(res.pca)
> ind
Principal Component Analysis Results for individuals
 ===================================================
  Name       Description                       
1 "$coord"   "Coordinates for the individuals" 
2 "$cos2"    "Cos2 for the individuals"        
3 "$contrib" "contributions of the individuals"
```
然后按照上面的模式来展示下individuals的点图，比如以cos2值来代表各个individuals点的圆圈大小
```
fviz_pca_ind(res.pca, pointsize = "cos2", 
     pointshape = 21, fill = "#E7B800",
     repel = TRUE # Avoid text overlapping (slow if many points)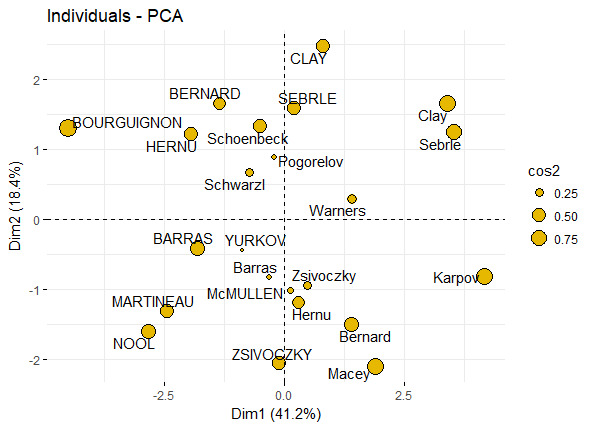
)
```
pca_ind_point

如果有分组信息，则可以将同一组的individuals圈在一起，如：
```
fviz_pca_ind(iris.pca,
     geom.ind = "point", # show points only (nbut not "text")
     col.ind = iris$Species, # color by groups
     palette = c("#00AFBB", "#E7B800", "#FC4E07"),
     addEllipses = TRUE, # Concentration ellipses
     legend.title = "Groups"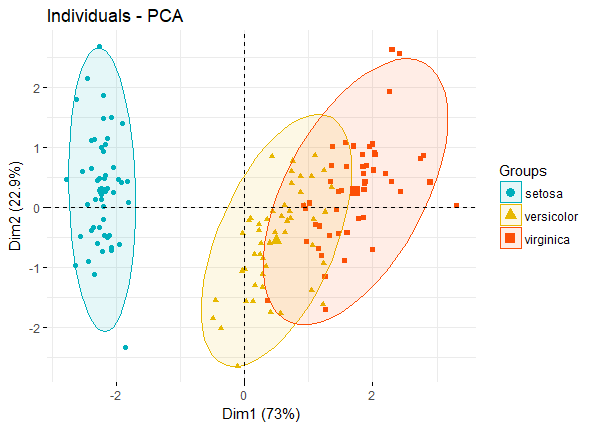
     )
```
pca_ind_group

上述图形可改进用于展示置信椭圆和不规则图形等

最后可以将vars和individuals同时在一张biplot图中展示（一般biplot图只用于展示变量较少的情况）
```
fviz_pca_biplot(iris.pca, 
        col.ind = iris$Species, palette = "jco", 
        addEllipses = TRUE, label = "var",
        col.var = "black", repel = TRUE,
        legend.title = "Species")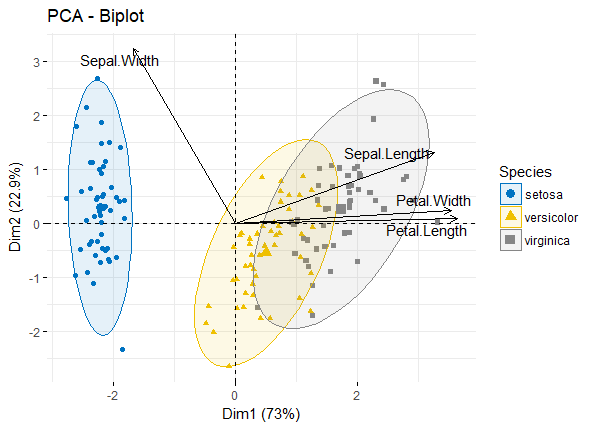
```
pca_biplot

Summary

这篇笔记我只是一个搬用工，这篇PCA - Principal Component Analysis Essentials文章对于PCA的分析（没怎么讲原理，只是单纯的使用和可视化）讲的真的不错，我挑了部分内容照搬了下，有意向的最好看原文哈

另外再推荐个PCA的原理讲解：StatQuest学习笔记14——PCA

本文出自于http://www.bioinfo-scrounger.com转载请注明出处