KeepNotes blog

Stay hungry, Stay Foolish.

0%

R语言 相关性分析

Posted on Edited on In
Symbols count in article: 4.2k Reading time ≈ 4 mins.

来自于 白话统计这本书的 一些笔记

相关系数是对变量之间的相关程度的定量描述，这里不得不提两个概念：协方差和相关系数

协方差和相关系数

协方差是一种用来衡量两个随机变量关系的统计量

formula1

其中：
X, Y是两个随机变量
μx, μy是两个随机变量的均值

如果两个变量是高度同向的，即X变大，Y也变大，那么对应的协方差也就很大；如果每次X变大，Y就变小，那么X和Y的协方差可能就会为负数

从公式中可看出，其实方差可以看作协方差的特例，即自己对自己的关系就是方差

但用协方差不利于度量单位不同的变量之间的比较，因此需要对变量进行标准化

formula1

那么转化为一般情况下的相关系数公式如下：

formula2

而这个线性相关系数计算方法正是我们常见的Pearson相关系数（事实上，首先提出的是Galton，但却是Pearson推广并发展的，因此仍以其名字命名）

还有一个表示相关程度的统计量则是决定系数（coefficient of determination）：是一个变量的方差能被另一个变量的方差解释的百分比；其值是相关系数r的平方

我们常见的Pearson相关系数除了适用于连续变量外，还可以用于无序的分类变量，但其有个前提是需要两个变量来自于正态分布的总体（这假设是其公式的前提条件）；当变量的总体不满足正态分布或者是有序的分类变量（等级资料）的话，则可以考虑用基于秩次的相关系数

基于秩次的相关系数主要有：

  • Spearman相关系数
  • Kendall的τ系数
  • γ系数

Spearman相关系数平时可能用的比较多，其思路是分别求出每个变量各自排序后的秩次，然后将秩次作为变量，从而计算这个秩次变量的Pearson相关系数（用的还是Pearson的计算公式）

相对于Pearson相关系数，Spearman相关系数对于数据错误和极端值的反应不敏感

相关系数检验

我们计算出来的相关系数一般是样本的统计量，需要进行假设检验从而推论到总体，这里可以用t检验来计算显著性，也可以用置信区间法

相关系数检验的原假设为：r=0，即两个变量之间无相关性

formula2

公式中，分子是样本统计量与参数值的差值，分母是线性相关系数的标准误，统计量t服从自由度为n-2的t分布，n为样本量

两个线性相关系数的比较可分为两种情况：

  • 两个独立样本之间的比较：如男性中体重与血压的相关系数r1和女性中体重与血压的相关系数r2的比较
  • 同一样本中的两个相关系数的比较：如体重与血压的相关系数r1和体重与血糖的相关系数r2的比较

R语言计算相关性以及显著性检验

测试数据，来源于美国50个州在1977年的人口，收入，文盲率，预期寿命，谋杀率以及高中毕业率的数据

states <- state.x77[,1:6]

我们可以用cor函数来计算相关性，method默认参数是用pearson；并且遇到缺失值，use默认参数everything，所以结果会是NA

比如计算下人口和收入这两个变量的相关性

> cor(x = states[,"Population"], y = states[,"Income"], use = "everything", method = "pearson")
[1] 0.2082276

可以对整个矩阵对个变量进行相关性计算，结果也是矩阵

> cor(states)
            Population     Income Illiteracy    Life Exp     Murder     HS Grad
Population  1.00000000  0.2082276  0.1076224 -0.06805195  0.3436428 -0.09848975
Income      0.20822756  1.0000000 -0.4370752  0.34025534 -0.2300776  0.61993232
Illiteracy  0.10762237 -0.4370752  1.0000000 -0.58847793  0.7029752 -0.65718861
Life Exp   -0.06805195  0.3402553 -0.5884779  1.00000000 -0.7808458  0.58221620
Murder      0.34364275 -0.2300776  0.7029752 -0.78084575  1.0000000 -0.48797102
HS Grad    -0.09848975  0.6199323 -0.6571886  0.58221620 -0.4879710  1.00000000

cor函数的method参数支持的相关性可选类型除了pearson外，还有spearman和kendall，如：

> cor(x = states[,"Population"], y = states[,"Illiteracy"], method = "spearman")
[1] 0.3130496

计算相关性的显著性则可以用cor.test函数，method默认是pearson，alternative默认是双尾（即总体相关系数不等于0）

> cor.test(x = states[,"Population"], y = states[,"Income"])

    Pearson's product-moment correlation

data:  states[, "Population"] and states[, "Income"]
t = 1.475, df = 48, p-value = 0.1467
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.07443435  0.45991855
sample estimates:
      cor 
0.2082276

从结果中可看到，cor.test不仅给了显著性的P值0.1467，还给出了置信区间[-0.0744, 0.4599]

提取P值和置信区间

res <- cor.test(x = states[,"Population"], y = states[,"Income"])
res$p.value
res$conf.int

但是cor.test只能用于计算两个变量的相关性检验，如果对多个变量或者矩阵数据的话，则可以使用psych包的corr.test函数

> corr.test(states, use = "complete", method = "pearson", adjust = "none")
Call:corr.test(x = states, use = "complete", method = "pearson", 
    adjust = "none")
Correlation matrix 
           Population Income Illiteracy Life Exp Murder HS Grad
Population       1.00   0.21       0.11    -0.07   0.34   -0.10
Income           0.21   1.00      -0.44     0.34  -0.23    0.62
Illiteracy       0.11  -0.44       1.00    -0.59   0.70   -0.66
Life Exp        -0.07   0.34      -0.59     1.00  -0.78    0.58
Murder           0.34  -0.23       0.70    -0.78   1.00   -0.49
HS Grad         -0.10   0.62      -0.66     0.58  -0.49    1.00
Sample Size 
[1] 50
Probability values (Entries above the diagonal are adjusted for multiple tests.) 
           Population Income Illiteracy Life Exp Murder HS Grad
Population       0.00   0.15       0.46     0.64   0.01     0.5
Income           0.15   0.00       0.00     0.02   0.11     0.0
Illiteracy       0.46   0.00       0.00     0.00   0.00     0.0
Life Exp         0.64   0.02       0.00     0.00   0.00     0.0
Murder           0.01   0.11       0.00     0.00   0.00     0.0
HS Grad          0.50   0.00       0.00     0.00   0.00     0.0

上半个矩阵是相关系数，下半个矩阵是显著性P值（我参数选择不校正的）

输出相关性和P值

res <- corr.test(states, use = "complete", method = "pearson", adjust = "none")
res$r
res$ci

可视化

相关系数矩阵可视化最常用的要属corrplot包了，简单看下可视化的图

library(corrplot)
res_cor <- cor(states)
corrplot(corr=res_cor)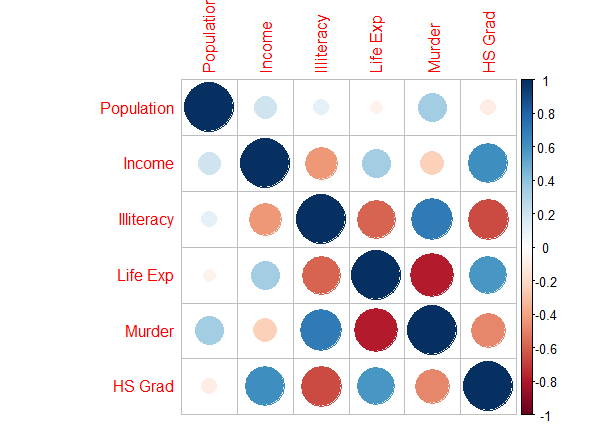
corrplot_1
corrplot(corr = res_cor,order = "AOE",type="upper",tl.pos = "d")
corrplot(corr = res_cor,add=TRUE, type="lower", method="number",order="AOE",diag=FALSE,tl.pos="n", cl.pos="n")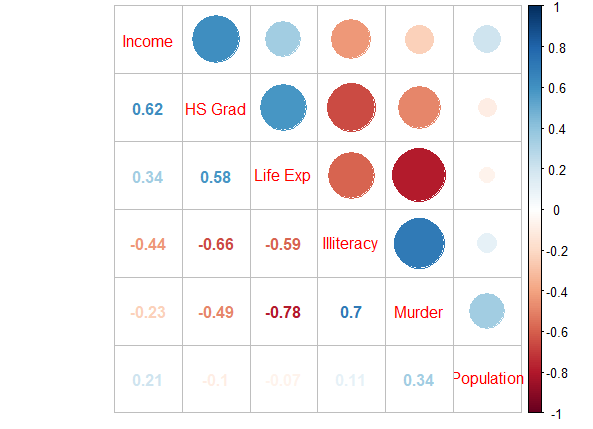
corrplot_2

除了属corrplot包外，PerformanceAnalytics包的chart.Correlation函数也是用于可视化相关系数矩阵的，从图上来看，其可以认为是基础包的pairs函数的加强版

chart.Correlation(states, method = "pearson")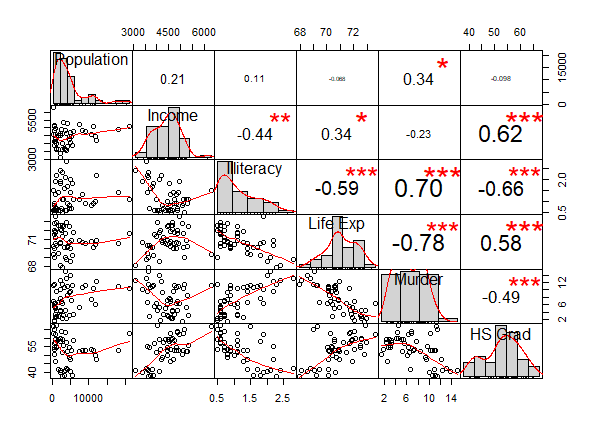
chart_correlation

参考资料：
Correlation and Linear Regression
markdown最全数学公式
生物统计专题：计算协方差与相关系数

本文出自于http://www.bioinfo-scrounger.com转载请注明出处

Related Posts