之前看到不少人思维导图,我也来凑凑热闹。用幕布做了一个,以做为这篇的笔记的总提纲
什么是方差分析
方差分析分析(Analysis of Variance),简写为ANOVA,不仅是一种方法,更是一种分析思路,是变异分解的思路。这种思路不仅可以用于多组均值差异的比较,也可以用于其他统计学方法中,比如线性回归、Logistic回归中也有方差分析 ——白话说统计
方差分析的基本思想
- 将数据的总变异分解为来源于不同因素的相应变异,从而明确各个变异因素在总变异中所占的重要程度
- 方差分析一般基于两类误差:随机误差和系统误差
- 随机误差:是指同一因素下,样本各观察值之间的差异,这种差异可以看做随机因素所引起的
- 系统误差:是指不同因素下,样本各观察值之间的差异,这种差异可能是由于抽样的随机性所引起的,也可能是因素所造成的(也就是系统性因素所造成的)
- 方差分析实质比较的是以上两类误差,这误差可以用组内(within groups)/组间(between groups)离差平方和表示
- 考虑到离差平方和会随着样本数增加而增大,所以将离差平方和转变为方差来表示
- 进而将其中的误差方差作为和其他因素方差比较的标准,从而推断总变异是由误差引起的还是由因素导致的
但是在方差分析中,我们是将所有样本响应变量的方差称为Total Sum of Squares(SST),也叫总离差平方和,全部观测值与总平均值的离差平方和,反映全部观测值的离散情况
由因素不同水平间差异引起的(可以由模型中因素解释的部分)方差称为Model Sum of Squares(SSM),也叫组间离差平方和,各组观测值的平均值与总平均值的离差平方和,反映各组样本均值之间的差异程度,包括随机误差和系统误差
由抽本过程本身所引起的部分方差称为Error Sum of Squares,(SSE),也叫组内离差平方和,各组观测值与其组平均值的离差平方和,反映组内各观测值的离散情况,也反映了随机误差的大小
\[ SST=SSM+SSE \]
如果我们想衡量上述SSM和SSE中哪个占显著比例,可以通过衡量上述两部分比例大小的统计量F
从上述离差平方和的公式(翻书哈)可看出,其大小跟观测值的数目有关,因此为了消除观测值数目对其的影响,需要将其平均,也就是转化为方差(离差平方和除以对应自由度);SST的自由度为n-1, 其中n为全部观测值的个数,SSM的自由度为k-1, 其中k为因子水平的个数,SSE的自由度为n-k
那么统计量F的计算方式如下:
\[ F=\frac{SSM/(k-1)}{SSE/(n-k)} \]
根据模型的自由度(k-1)以及误差自由度(n-k),可以确定一个F分布;再由上述公式计算出的F0进一步确定P值;再根据显著性水平来判断是否能拒绝原假设
方差分析的前提假设:
- 样本数据独立
- 每组数据的总体服从正态分布
- 每组数据方差齐性
样本数据独立与否比较好判断,根据实验设计来即可确定,保证每组数据之间无关联即可
正态性检验:
- 使用Shapiro-Wilk正态检验方法来检验样本是否符合正态分布
- 使用Q-Q图来检验正态性
方差齐性检验:
- Bartlett检验,适用于数据服从正态分布;而当数据非正态时则容易导致假阳性
- Levene检验,在非正态数据表现较为稳健,对正态不敏感
- Fligner-Killeen检验,非参数检验,完全不依赖已知分布
离群点检验:
由于方差分析对离群点很敏感,所以需要对数据检测是否有离群点,最常用(可能也较为好使的)是以图形展示,如箱线图、散点图等形式:
- aq.plot()作图
- car包的outlierTest()检测
在实际应用,特别是生物统计中,往往并不要求数据严格服从正态分布(因为方差分析对正态不是很敏感,特别是对单因素方差分析);如果数据近似服从正态分布(当样本数足够多的时候,一般认为观测的分布是服从正态的),或者对数据进行一定的变化,使其接近于正态分布
如果数据不符合方差齐性,可以参看方差分析为何要进行方差齐次检验?中提到的Handbook of Biological Statistics,作者认为在每组样本数平衡的情况下,单因素方差分析对方差齐性不敏感,除非标准差相差3倍以上并且样本数小于10个,不然假阳性还是比较低的。当然,如果样本数不平衡以及标准差相差较大的情况下,可以考虑使用Welch's anova,R语言的oneway.test()函数以将其封装进去了
如果正态分布也不满足,方差齐性也不满足,可以使用非参的秩和检验kruskal.test(),但是有时针对单因素方差分析而言,kruskal.test()并不好使,还不如使用Welch's anova
单因素方差分析
单因素方差分析是方差分析中最容易理解的一种方法了,其主要为了检验在一个因素的多个水平下各组均值的差异
以R中的数据集PlantGrowth为例,来将上面所说的内容都实现下
先初步展示下数据,其包含了植物在空白(ctrl)以及两个处理下(trt1,trt2)的植物的重量数据
data <- PlantGrowth
>head(data)
weight group
1 4.17 ctrl
2 5.58 ctrl
3 5.18 ctrl
4 6.11 ctrl
5 4.50 ctrl
6 4.61 ctrl再看下散点图分布
library("ggpubr")
ggline(data, x = "group", y = "weight",
add = c("mean_se", "jitter"),
order = c("ctrl", "trt1", "trt2"),
ylab = "Weight", xlab = "Treatment")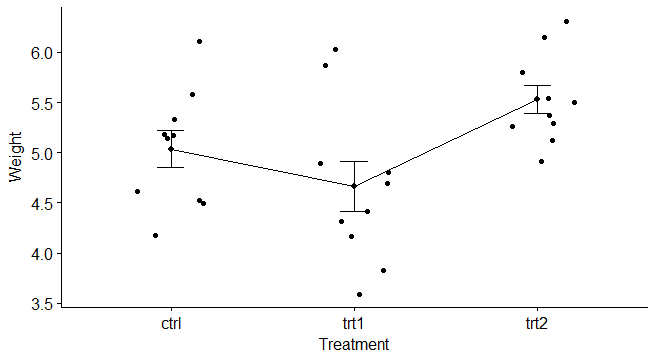
接着正态检验(对3个水平下的每组数据都做一次正态检验),可看出P值均大于0.05,都满足正态分布
group_data <- split(data[,1], data[,2])
>unlist(lapply(group_data, function(x){
shapiro.test(x)$p.value
}))
# ctrl trt1 trt2
0.7474734 0.4519440 0.5642519 去其中ctrl组做个Q-Q图
library(car)
qqPlot(group_data[[1]])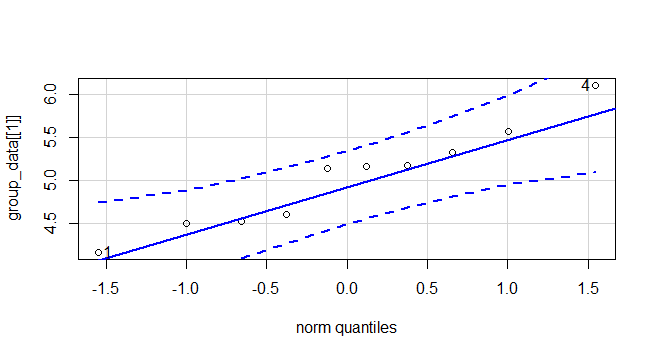
方差齐性检验,使用car包的leveneTest(),可看出,P值大于0.05,满足方差齐性
> leveneTest(weight~group, data = data)
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 2 1.1192 0.3412
27查看是否有离群点
> outlierTest(lm(weight~group, data=data))
No Studentized residuals with Bonferonni p < 0.05
Largest |rstudent|:
rstudent unadjusted p-value Bonferonni p
17 2.537341 0.017509 0.52526最后使用aov函数进行单因素方差分析,结果显示P值小于0.05,说明不同处理对植物的重量有显著影响
> summary(aov(weight~group, data = data))
Df Sum Sq Mean Sq F value Pr(>F)
group 2 3.766 1.8832 4.846 0.0159 *
Residuals 27 10.492 0.3886
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
pvalue <- summary(aov(weight~group, data = data))[[1]][,"Pr(>F)"][1]
> pvalue
[1] 0.01590996Df为自由度,Sum Sq为总方差和,Mean Sq为平均方差和,F value为F统计量,Pr(>F)为P值
如果方差不齐性(并且每组样本数也不平衡),那么可以使用oneway.test(),Welch's anova相当于根据每组方差加了个不同的权重调整了F统计量
> oneway.test(weight~group, data = data, var.equal = F)
One-way analysis of means (not assuming equal variances)
data: weight and group
F = 5.181, num df = 2.000, denom df = 17.128, p-value = 0.01739
> oneway.test(weight~group, data = data, var.equal = F)$p.value
[1] 0.01739282单因素方差分析中还有一种是单因素协方差分析,简单的提一下,以multcomp包中litter数据集为例,该数据集将怀孕小鼠分为4组,每组接受不同剂量的药物处理(dose值),dose为自变量,生出的幼崽体重(weight)为因变量,怀孕时间(gesttime)为协变量,那么用aov()函数协方差分析如下:
> summary(aov(weight~gesttime+dose,data = litter))
Df Sum Sq Mean Sq F value Pr(>F)
gesttime 1 134.3 134.30 8.049 0.00597 **
dose 3 137.1 45.71 2.739 0.04988 *
Residuals 69 1151.3 16.69
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1这里aov的函数顺序有点要求,需要将协方差写在前面,接着是自变量,然后是双因素的交互项等等(如果是双因素协方差分析的话。。。),从上结果可看出:gesttime与weight相关,在控制gesttime后,dose与weight相关
获得去除协变量效应后的组均值:
> effect("dose", aov(weight~gesttime+dose,data = litter))
dose effect
dose
0 5 50 500
32.35367 28.87672 30.56614 29.33460 协方差分析和方差分析一样,都需要正态性和同方差性假设,前者还假定回归斜率相同,所以需要检验下回归斜率的同质性,以本数据集为例,原假设则是斜率相同,其意思就是每组通过怀孕时间来预测出生体重的回归斜率都相同
> summary(aov(weight~gesttime*dose,data = litter))
Df Sum Sq Mean Sq F value Pr(>F)
gesttime 1 134.3 134.30 8.289 0.00537 **
dose 3 137.1 45.71 2.821 0.04556 *
gesttime:dose 3 81.9 27.29 1.684 0.17889
Residuals 66 1069.4 16.20
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1通过上述结果可看出:gesttime和dose交互作用不显著,因此原假设成立;因为如果交互作用显著,则说明怀孕时间与出生体重的关系依赖于药物剂量dose,那么需要使用非参协方差分析函数(不需要假设回归斜率同质性),如sm包的sm.ancova()函数
用HH包可视化下结果,ancova()函数可以绘制因变量、协变量和因子之间的关系图
> ancova(weight~gesttime+dose,data = litter)
Analysis of Variance Table
Response: weight
Df Sum Sq Mean Sq F value Pr(>F)
gesttime 1 134.30 134.304 8.0493 0.005971 **
dose 3 137.12 45.708 2.7394 0.049883 *
Residuals 69 1151.27 16.685
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1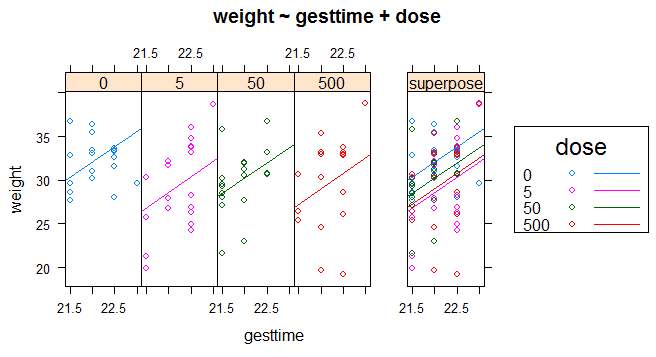
从上图可看出:用怀孕时间来预测出生体重的回归线相互平行(因为之间检验的了回归斜率的同质性,因此只是截距项不同),随着怀孕时间增加,幼崽出生体重也会增加;还可以看到dose与weight的关系,0剂量组截距项最大,5剂量组截距项最小
PS. 若用anvova(weight~gesttime*dose),生成的图形将允许斜率和截距项依据组别而发生变化,这对可视化那些违背回归斜率同质性的实例非常有用
双因素方差分析
如果不考虑双因素之间的交互作用的话,那么双因素方差分析和单因素方差分析没啥区别
以一个R数据集为例来看看如何分析双因素的交互作用(有重复)
data <- ToothGrowth
> str(data)
'data.frame': 60 obs. of 3 variables:
$ len : num 4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
$ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
$ dose: num 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...可看出ToothGrowth数据集的dose列并没有设为因子,而后续双因素方差分析其中一个因素就是dose,因此需将其设为因子(不然结果是错误的!)
data$dose <- factor(data$dose, levels = c(0.5,1,2), labels = c("D0.5", "D1", "D2"))粗略用点线图展示下
library("ggpubr")
ggline(data, x = "dose", y = "len", color = "supp",
add = c("mean_se", "dotplot"),
palette = c("#00AFBB", "#E7B800"))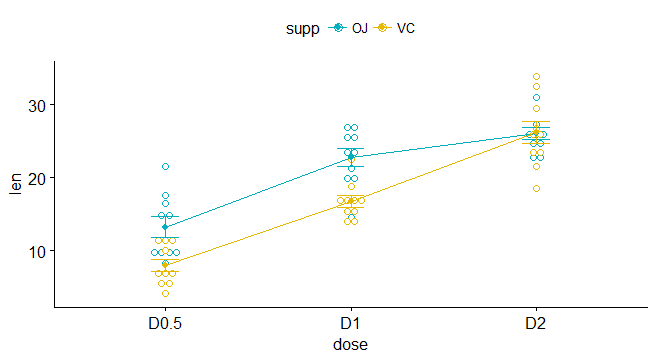
接着就是用aov()来双因素方差分析
> summary(aov(len ~ supp * dose, data = data))
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205.4 205.4 15.572 0.000231 ***
dose 2 2426.4 1213.2 92.000 < 2e-16 ***
supp:dose 2 108.3 54.2 4.107 0.021860 *
Residuals 54 712.1 13.2
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1从上述结果看跟单因素差别在于其还有了个交互作用的结果(主要其原假设中就是假设没交互作用),各个因素的自由度也是其水平数减1,supp:dose对应的行则是其交互作用的结果
HH包可视化展示
interaction2wt(len~supp*dose)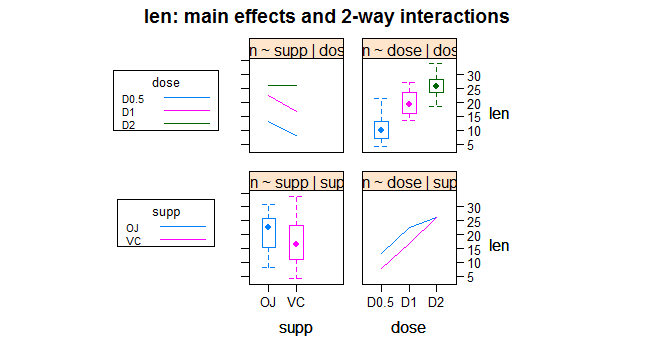
这张图分别展示了任意顺序的因素和其交互作用
资源:
一个不错的学习用R进行统计分析的网站http://www.sthda.com/english/wiki/comparing-means-in-r,文字表达简单易懂哈
还有一个大神总结的方差分析资料方差分析,可以另存为下来本地慢慢看
参考资料:
方差分析
R语言方差分析ANOVA
应用统计学与R语言实现学习笔记(八)——方差分析
【r<-高级|实战|统计】R中的方差分析ANOVA
【数据分析 R语言实战】学习笔记 第八章 方差分析与R实现
http://www.biostathandbook.com/onewayanova.html
方差分析(一): 方差分析的基本原理
本文出自于http://www.bioinfo-scrounger.com转载请注明出处
