实验设计中,一般会做三个生物学重复来确保结果的准确性,尤其在下游分析中。但有时会遇到没有生物学重复,而又需要进行差异分析的情况,这时一般建议考虑foldchange即可,因为根本无法进行T-test等统计学方法嘛。但是如果必须要算一个P值(个人觉得没啥必要。。。),那么不同组学有各自处理的方法(虽然并不是靠谱),比如NGS的转录组的一些软件会预估一个离散度做校正,而质谱的蛋白组则是用Significance A/B算法,这篇文章主要讲下Significance A/B是怎么来的 一般在网上搜Significance A/B是很难搜到相关信息的,因为这个是特定用于蛋白组学的一种统计学方法,而且现在来说用的也比较少了;那当初为何提出这分析方法,个人觉得可能是因为那时蛋白组学成本过高。以前一直只知道有这一分析方法,但是不知其原理,最近在搜索中无意发现一个帖子What statistical methods for ITRAQ with two biological replication?,其中提到一篇文章中有对Significance A/B的介绍
Significance A/B最先是发表于2008年Nature Biotechnology期刊上,MaxQuant enables high peptide identification rates, individualized p.p.b.-range mass accuracies and proteome-wide protein quantification,这篇文章主要是介绍Maxquant这款用于蛋白组定量分析软件的,非常有名,而其附录中作者提到了如何通过protein ratio来计算显著性(P值),附录PDF
先明确下Significance A/B算法的理论基础,原文如下:
The assumption that the ratio distribution is normal in a case where no differential regulation takes place is reasonable, since the protein ratios are obtained as averages of many SILAC peptide ratios. In the limit of a large number of SILAC peptides per protein a normal distribution can be assumed due to the central limit theorem
我的理解是,作者认为由于protein ratio是根据每个protein下许多个peptide的ratio计算出来的,那么根据中心极限定理,这ratio被假定为符合正态分布是合理的
什么是中心极限定理,引用<白话统计>书中的解释(因为我觉得这个更加通俗一点):
中心极限定理不是针对原始数据的,而是针对统计量的。它说的是:不管原始数据的分布是什么样的(可能是正态的,也可能是偏态的),从原始数据中多次抽样,得到多个样本,每个样本可以计算出一个相应的统计量(如均数),如果每个样本中的例数大于30,那么这些统计量(如均数)的分布接近正态分布;而不是说:一个样本中的原始数据的个数大于30,原始数据的分布接近正态
所以根据上述中心极限定理,作者认为一个protein的ratio值是根据N个peptide的ratio计算出的一个统计量,这里的protein可以被看做一次抽样,而N个peptide则被看作是一次抽样中的N个例数,因此所有protein的ratio的分布可以被假定为正态分布。(PS.虽然理论基础还是蛮合理的,但是其实真正应用时并不是均符合的,比如不是所有protein的peptide都大于30个,另外在一些情况下是直接使用protein的intensity value来计算ratio,而不是基于peptide,仅为个人观点。。)
那么Significance A/B是如何计算的呢,先简单的讲一下Significance A,而Significance B则类似
Significance A
从上述的理论基础可看出,作者假定ratio的分布是符合正态分布的,那么根据正态分布的公式,我们需要对个每个protein的ratio做些处理以及标准化
The base of the logarithm is irrelevant for our calculation,对每个ratio作log转换,至于log2还是log10都可以,不影响结果
To make a robust and asymmetrical estimate of the standard deviation of the main distribution we calculate the 15.87, 50, and 84.13 percentiles r-1, r0, and r1,为了估计一个健壮以及不对称的标准差,作者先计算了15.87,50,84.34三个百分位的值,然后根据下述公式做标准化获得一个Z值,其中
r1-r0和r0-r-1则是分布左右两边的标准差。因此当ratio值大于ro时,标准差则为r1-r0;而当ratio值小于ro时,标准差则为r0-r-1,具体公式如下图所示: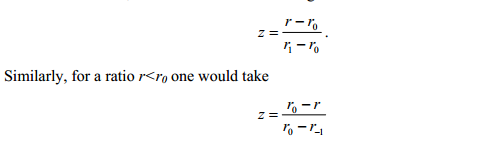
significance-z-value Under the null hypothesis of normal tails of the log ratio distribution the probability of obtaining a value this large or larger is,将ratio做标准化转化后,这时的Z值则符合标准正态分布了,那么其对应的概率计算则就变得很简单了,类似于标准的假设检验方法了,按照作者意思,计算在正态分布中大于Z值的概率(标准正态分布曲线下大于Z值的那部分面积),可以理解为假设检验中的单尾检验?具体公式如下,其实就是个标准正态分布的概率累计函数
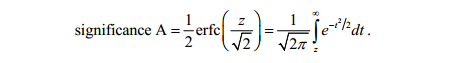
significance-pvalue
Significance B
Significance B的计算过程类似于Significance A,或者说是改进版?
作者发现那些高丰度蛋白相比低丰度蛋白,其中未发生变化的蛋白的ratio分布更加集中,如下图所示,那么高丰度蛋白的ratio也就相对会更加显著
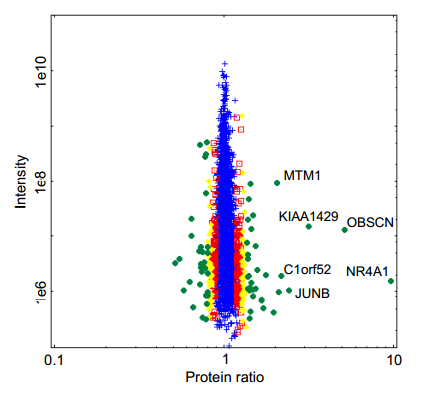
significance_plot 考虑到这个丰度对结果影响,作者在Significance A算法的基础上,将protein根据intensity分成N个bin,每个bin至少包含300个蛋白,最后对每个bin进行一遍Significance A计算,然后将结果整合在一起
代码实现
了解了上述的Significance A/B的计算过程,那么我们就可以用代码将其实现,下面我用R写了个函数来计算Significance A,而Significance B从上述可知,只要对protein分bin后再用Significance A计算即可(这里不重复展示了),输入为ratio向量
get_significance <- function(ratio){
ratio <- log2(as.numeric(ratio))
order_ratio <- ratio[order(ratio)]
quantiletmp <- quantile(order_ratio, c(0.1587,0.5,0.8413))
rl <- as.numeric(quantiletmp[1]) #对应公式中的r-1
rm <- as.numeric(quantiletmp[2]) #对应公式中的r0
rh <- as.numeric(quantiletmp[3]) #对应公式中的r1
p <- unlist(lapply(ratio, function(x){
if (x > rm){
z <- (x-rm)/(rh-rm)
pnorm(z,lower.tail = F)
}else{
z <- (rm-x)/(rm-rl)
pnorm(z,lower.tail = F)
}
}))
}接着用这个函数计算ratio值就可得对应的P值了
p <- get_significance(data)以上为个人的理解,具体可以看那篇文献哦
本文出自于http://www.bioinfo-scrounger.com转载请注明出处